
分析 (1)利用一次函数、二次函数的图象与性质即可得出.
(2)设t时刻的纯收益为h(t),则h(t)=f(t)-g(t),即h(t)=$\left\{\begin{array}{l}{-\frac{1}{200}{t}^{2}+\frac{1}{2}t+\frac{175}{2},0≤t≤200}\\{-\frac{1}{200}{t}^{2}+\frac{7}{2}t-\frac{1025}{2},200<t≤300}\end{array}\right.$,利用二次函数的单调性即可得出.
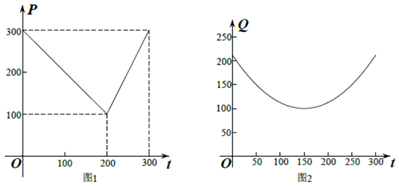
解答 解:(1)由图1可得市场售价与时间的函数关系为f(t)=$\left\{\begin{array}{l}{300-t,0≤t≤200}\\{2t-300,200<t≤300}\end{array}\right.$,
由图2可得种植成本与时间的函数关系式为g(t)=$\frac{1}{200}$(t-150)2+100,0≤t≤300;
(2)设t时刻的纯收益为h(t),则h(t)=f(t)-g(t),
即h(t)=$\left\{\begin{array}{l}{-\frac{1}{200}{t}^{2}+\frac{1}{2}t+\frac{175}{2},0≤t≤200}\\{-\frac{1}{200}{t}^{2}+\frac{7}{2}t-\frac{1025}{2},200<t≤300}\end{array}\right.$,
当0≤t≤200时,配方整理得h(t)=-$\frac{1}{200}$(t-50)2+100,
所以,当t=50时,h(t)取得区间[0,200]上的最大值100;
当200<t≤300时,配方整理得h(t)=-$\frac{1}{200}$(t-350)2+100,
所以,当t=300时,h(t)取得区间(200,300]上的最大值87.5;
综上所述,纯收益最大值为100元,此时t=50,即从二月一日开始的第50天时,上市的西红柿收益最答.
点评 本题考查了一次函数、二次函数的图象与性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -4 | C. | -5 | D. | $-\frac{15}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10π | B. | 22π | C. | 24π | D. | 28π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)>1,则$\frac{b+1}{a+1}$的取值范围是( )
定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)>1,则$\frac{b+1}{a+1}$的取值范围是( )| A. | ($\frac{1}{5}$,$\frac{1}{3}$) | B. | (-∞,3) | C. | (-∞,$\frac{1}{3}$) | D. | ($\frac{1}{3}$,5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com