
【题目】执行所给的程序框图,则输出的值是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
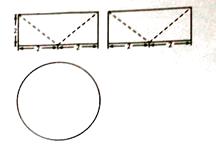
【题目】祖冲之之子祖暅是我国南北朝时代伟大的科学家,他在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”.意思是,如果两个等高的几何体 在同高处截得的截面面积恒等,那么这两个几何体的体积相等.此即祖暅原理.利用这个原理求球的体积时,需要构造一个满足条件的几何体,已知该几何体三视图 如图所示,用一个与该几何体的下底面平行相距为 h(0<h<2) 的平面截该几何体,则截面面积为 ( )
A.![]()
B.![]()
C.![]()
D.π(4-h2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() 的最大值为2,它的最小正周期为2π. (Ⅰ)求函数f(x)的解析式;
的最大值为2,它的最小正周期为2π. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)若g(x)=cosxf(x),求g(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的离心率为
的离心率为 ![]() ,M为C上除长轴顶点外的一动点,以M为圆心,
,M为C上除长轴顶点外的一动点,以M为圆心, ![]() 为半径作圆,过原点O作圆M的两条切线,A、B为切点,当M为短轴顶点时∠AOB=
为半径作圆,过原点O作圆M的两条切线,A、B为切点,当M为短轴顶点时∠AOB= ![]() . (Ⅰ)求椭圆的方程;
. (Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆的右焦点为F,过点F作MF的垂线交直线x= ![]() a于N点,判断直线MN与椭圆的位置关系.
a于N点,判断直线MN与椭圆的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量y(g)与尺寸x(mm)之间近似满足关系式y=axb(a,b为大于0的常数).现随机抽取6件合格产品,测得数据如下:
尺寸(mm) | 38 | 48 | 58 | 68 | 78 | 88 |
质量(g) | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
对数据作了初步处理,相关统计量的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(Ⅰ)根据所给数据,求y关于x的回归方程;
(Ⅱ)按照某项指标测定,当产品质量与尺寸的比在区间( ![]() ,
, ![]() )内时为优等品.现从抽取的6件合格产品中再任选3件,记ξ为取到优等品的件数,试求随机变量ξ的分布列和期望.
)内时为优等品.现从抽取的6件合格产品中再任选3件,记ξ为取到优等品的件数,试求随机变量ξ的分布列和期望.
附:对于一组数据(v1 , u1),(v2 , u2),…,(vn , un),其回归直线u=α+βv的斜率和截距的最小二乘估计分别为 ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且2Sn=4an﹣1. (Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=anan+1﹣2,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名篮球运动员在7场比赛中的得分情况如茎叶所示, ![]() 甲、
甲、 ![]() 乙分别表示甲、乙两人的平均得分,则下列判断正确的是( )
乙分别表示甲、乙两人的平均得分,则下列判断正确的是( ) 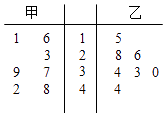
A.![]() 甲>
甲> ![]() 乙 , 甲比乙得分稳定
乙 , 甲比乙得分稳定
B.![]() 甲>
甲> ![]() 乙 , 乙比甲得分稳定
乙 , 乙比甲得分稳定
C.![]() 甲<
甲< ![]() 乙 , 甲比乙得分稳定
乙 , 甲比乙得分稳定
D.![]() 甲<
甲< ![]() 乙 , 乙比甲得分稳定
乙 , 乙比甲得分稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在海岸线 ![]() 一侧有一休闲游乐场,游乐场的前一部分边界为曲线段
一侧有一休闲游乐场,游乐场的前一部分边界为曲线段 ![]() ,该曲线段是函数
,该曲线段是函数 ![]() ,
, ![]() 的图像,图像的最高点为
的图像,图像的最高点为 ![]() .边界的中间部分为长1千米的直线段
.边界的中间部分为长1千米的直线段 ![]() ,且
,且 ![]() .游乐场的后一部分边界是以
.游乐场的后一部分边界是以 ![]() 为圆心的一段圆弧
为圆心的一段圆弧 ![]() .
.
(1)求曲线段 ![]() 的函数表达式;
的函数表达式;
(2)曲线段 ![]() 上的入口
上的入口 ![]() 距海岸线
距海岸线 ![]() 最近距离为1千米,现准备从入口
最近距离为1千米,现准备从入口 ![]() 修一条笔直的景观路到
修一条笔直的景观路到 ![]() ,求景观路
,求景观路 ![]() 长;
长;
(3)如图,在扇形 ![]() 区域内建一个平行四边形休闲区
区域内建一个平行四边形休闲区 ![]() ,平行四边形的一边在海岸线
,平行四边形的一边在海岸线 ![]() 上,一边在半径
上,一边在半径 ![]() 上,另外一个顶点P在圆弧
上,另外一个顶点P在圆弧 ![]() 上,且
上,且 ![]() ,求平行四边形休闲区
,求平行四边形休闲区 ![]() 面积的最大值及此时
面积的最大值及此时 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com