
求以下两函数的最大值.
(1)y=5sin(x+![]() )+3sin(x+
)+3sin(x+![]() );
);
(2)y=![]() +
+![]() sin2x.
sin2x.
|
思路 设法配凑化简为基本型.若能化成acosx+bsinx型.当x∈R时,其最大值即为 解答 (1)y=5sin[(x+ = ∵x∈R∴y最大值= (2)∵sin3x·sin3x+cos3x·cos3x =(3sinx-4sin3x)sin3x+(4cos3x-3cosx)·cos3x =3(sin4x-cos4x)+4(cos6x-sin6x) =-3cos2x+4cos2x(1-cos2xsin2x) =cos2x(1-sin22x)=cos32x ∴原式= ∴y最大值=2 评析 在(2)中sin3x可以用sin(2x+x)形式展开,也可以将sin3x写出sinx·sin2x,再使sin3x与sinx结合使用积化和差公式. |


科目:高中数学 来源: 题型:
| 4x |
| x2+a |
| y | 0 | 0.1 | 0.2 | 0.5 | 0.8 | 1 | 1.2 | 1.5 | 1.8 | 2 | 4 | 6 | … |
| y | 0 | 0.396 | 0.769 | 1.6 | 1.951 | 2 | 1.967 | 1.846 | 1.698 | 1.6 | 0.941 | 0.649 | … |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4x |
| a |
| 2x |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省高三上学期期中理科数学试卷(解析版) 题型:解答题
(本小题满分13分)
已知函数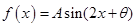 ,其中
,其中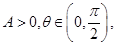 请分别解答以下两小题.
请分别解答以下两小题.
(Ⅰ)若函数过点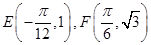 ,求函数
,求函数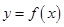 的解析式.
的解析式.
(Ⅱ)如图,点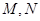 分别是函数
分别是函数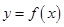 的图像在
的图像在 轴两侧与
轴两侧与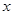 轴的两个相邻交点, 函数图像上的一点
轴的两个相邻交点, 函数图像上的一点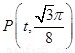 ,若满足
,若满足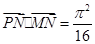 ,求函数
,求函数 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com