
已知cosα=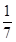 ,cos(α-β)=
,cos(α-β)=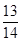 ,且0<β<α<
,且0<β<α<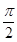 .
.
(1)求tan2α的值;
(2)求β的值.
(1) -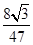 (2)
(2) 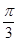
【解析】本试题主要是考查了两角和差的三角函数变换的运用,以及构造角的思想求解角的 综合运用。
(1)由cosα=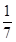 ,0<α<
,0<α<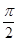 ,
,
得sinα=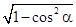 =
=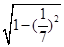 =
=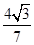 ,
,
∴tanα=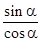 =
=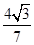 ×
×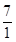 =
=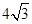 .
.
从而结合二倍角公式得到结论。
(2)由β=α-(α-β)
cosβ=cos[α-(α-β)]
=cosαcos(α-β)+sinαsin(α-β)= 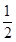
那么利用由0<β<α<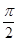 ,得0<α-β<
,得0<α-β<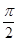 .
.
又∵cos(α-β)=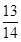 ,得到各个三角函数值,求解得到结论。
,得到各个三角函数值,求解得到结论。
(1)由cosα=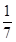 ,0<α<
,0<α<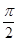 ,
,
得sinα=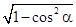 =
=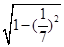 =
=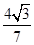 ,
,
∴tanα=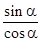 =
=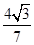 ×
×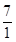 =
=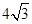 .
.
于是tan2α=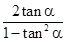 =
=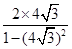
=-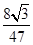 . ………6分
. ………6分
(2)由0<β<α<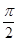 ,得0<α-β<
,得0<α-β<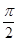 .
.
又∵cos(α-β)=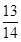 ,
,
∴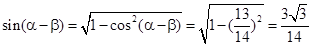
由β=α-(α-β)
cosβ=cos[α-(α-β)]
=cosαcos(α-β)+sinαsin(α-β)= 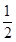
又∵0<β<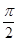
∴β= 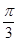 ……13分
……13分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年河南省原名校高三上学期期联考理科数学试卷(解析版) 题型:选择题
已知向量 =(cosθ,sinθ),向量
=(cosθ,sinθ),向量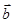 =(
=(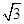 ,-1),则|2
,-1),则|2 -
-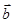 |的最大值与最小值的和是( )
|的最大值与最小值的和是( )
A.4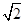 B.6
C.4
D.16
B.6
C.4
D.16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com