
(本小题满分14分)
如图,沿等腰直角三角形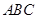 的中位线
的中位线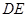 ,将平面
,将平面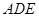 折起,平面
折起,平面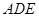 ⊥平面
⊥平面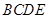 ,得到四棱锥
,得到四棱锥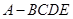 ,
,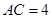 ,设
,设 、
、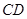 的中点分别为
的中点分别为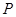 、
、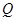 ,
,

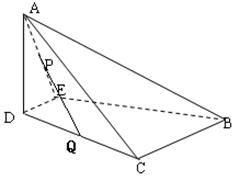
(1)求证:平面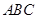 ⊥平面
⊥平面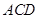
(2)求证:
(3)求平面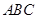 与平面
与平面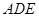 所成锐二面角的余弦值。
所成锐二面角的余弦值。
(1)见解析(2)见解析(3)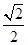
【解析】
试题分析:(1)证明: 平面
平面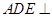 平面
平面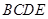 ,交线为
,交线为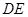 ,
,
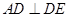 ,
,
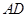
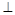 平面
平面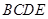 .
.

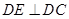 ,
,
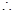
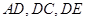 两两互相垂直,
两两互相垂直,
以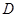 为原点建立空间直角坐标系,
……2分
为原点建立空间直角坐标系,
……2分
因为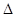
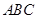 为等腰直角三角形,且
为等腰直角三角形,且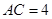 ,则
,则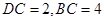 ,
,
则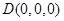 ,
,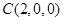 ,
,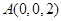 ,
,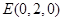 ,
,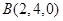 .
.
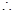
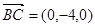 ,
, ,
,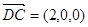 ,
,
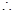
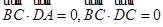 ,
,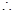
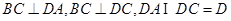 ,
,
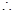
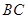
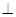 平面
平面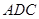 ,又
,又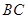
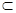 平面
平面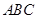
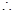 平面
平面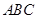 ⊥平面
⊥平面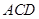 .
……5分
.
……5分
(2)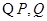 分别为
分别为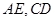 的中点,
的中点,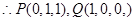 ,
,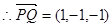 .
.
设平面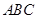 的法向量
的法向量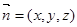 ,由于
,由于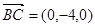
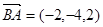
则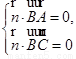 即
即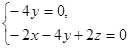 ,
,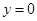 ,令
,令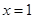 ,则
,则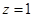 ,
,
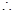
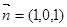 .
.
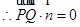 ,
即
,
即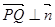
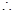
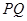 //平面
//平面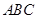 .
……9分
.
……9分
(3)由(2)可知平面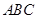 的法向量
的法向量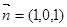 ,由于平面
,由于平面 的法向量为
的法向量为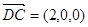 ,
,
设平面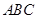 与平面
与平面 所成锐二面角为
所成锐二面角为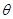 ,则
,则
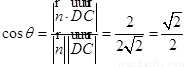 .
……14分
.
……14分
考点:本小题主要考查线面垂直、线面平行的判定以及二面角的求法,考查了逻辑思维能力与空间想象能力.
点评:求二面角最常用的方法就是分别求出二面角的两个面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,如果题目中没有说明,则要注意结合实际图形判断所求角是锐角还是钝角.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
| 3 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)设椭圆C1的方程为![]() (a>b>0),曲线C2的方程为y=
(a>b>0),曲线C2的方程为y=![]() ,且曲线C1与C2在第一象限内只有一个公共点P。(1)试用a表示点P的坐标;(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式。
,且曲线C1与C2在第一象限内只有一个公共点P。(1)试用a表示点P的坐标;(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式。
查看答案和解析>>
科目:高中数学 来源:2011年江西省抚州市教研室高二上学期期末数学理卷(A) 题型:解答题
(本小题满分14分)
已知 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
.
(1)证明:数列 }是等比数列;
}是等比数列;
(2)设 ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式;
(3)记 ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
.
查看答案和解析>>
科目:高中数学 来源:2015届山东省威海市高一上学期期末考试数学试卷(解析版) 题型:解答题
(本小题满分14分)
某网店对一应季商品过去20天的销售价格及销售量进行了监测统计发现,第 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 天的销售量为
天的销售量为 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元.
(Ⅰ)写出销售额 关于第
关于第 天的函数关系式;
天的函数关系式;
(Ⅱ)求该商品第7天的利润;
(Ⅲ)该商品第几天的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省高三下学期第一次月考文科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行.
⑴ 求 ,
, 满足的关系式;
满足的关系式;
⑵ 若 上恒成立,求
上恒成立,求 的取值范围;
的取值范围;
⑶ 证明: (
( )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com