
分析 (1)化简三角函数式并进行配方,结合正弦函数的有界性求值域;
(2)结合(1)的解析式以及角度范围求出方程$-(cosx+\frac{1}{2})^{2}+a+\frac{5}{4}$=0在(0,$\frac{π}{2}$)有解的关于a 的不等式,解之即可.
解答 解:(1)f(x)=sin2(π+x)-cos(2π-x)+a
=sin2x-cosx+a=-cos2x-cosx+a+1=$-(cosx+\frac{1}{2})^{2}+a+\frac{5}{4}$,x∈R,cosx∈[-1,1],
所以cosx=$-\frac{1}{2}$时,f(x)最大值为$a+\frac{5}{4}$,cosx=1时,f(x)最小值为-1+a;
所以f(x)的值域[-1+a,a+$\frac{5}{4}$];
(2)若f(x)在(0,$\frac{π}{2}$)内有零点,
$-(cosx+\frac{1}{2})^{2}+a+\frac{5}{4}$=0在(0,$\frac{π}{2}$)有解,
又(cosx+$\frac{1}{2}$)2∈($\frac{1}{4},\frac{9}{4}$),
所以$\frac{1}{4}$<a+$\frac{5}{4}$<$\frac{9}{4}$,解得-1<a<1.
点评 本题考查了三角函数的化简、三角函数的有界性以及三角函数的零点;注意角度范围对值域的影响.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
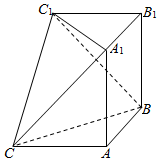 如图,AA1,BB1均垂直于平面ABC和平面A1B1C1,∠BAC=∠A1B1C1=90°,AC=AB=A1A=B1C1=$\sqrt{2}$,则多面体ABC-A1B1C1的外接球的表面积为( )
如图,AA1,BB1均垂直于平面ABC和平面A1B1C1,∠BAC=∠A1B1C1=90°,AC=AB=A1A=B1C1=$\sqrt{2}$,则多面体ABC-A1B1C1的外接球的表面积为( )| A. | 2π | B. | 4π | C. | 6π | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AD}$=-$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | B. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AD}$=-$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 以上都可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com