
设z是虚数,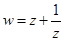 是实数,且
是实数,且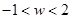 .
.
(1)求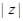 的值及z的实部的取值范围.
的值及z的实部的取值范围.
(2)设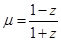 ,求
,求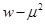 的最小值.
的最小值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
实数m分别取什么数值时,复数z=(m2+5m+6)+(m2-2m-15)i
(1)与复数2-12i相等;
(2)与复数12+16i互为共轭复数;
(3)对应的点在x轴的上方.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知m∈R,设p:复数z1=(m-1)+(m+3)i (i是虚数单位)在复平面内对应的点在第二象限,q:复数z2=1+(m-2)i的模不超过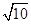 .
.
(1)当p为真命题时,求m的取值范围;
(2)若命题“p且q”为假命题,“p或q”为真命题,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com