考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)由题意知AA
1,AB,AC两两垂直,建立空间直角坐标系,利用向量法能证明AB
1∥平面C
1A
1C.
(2)设存在一点E,使BE⊥平面A
1CC
1,设
=λ
,由此利用向量法能求出线段CC
1上存在一点E,满足
=
,使BE⊥平面A
1CC
1.
(3)求出平面C
1A
1C的法向量和平面A
1CA的一个法向量,利用向量法能求出平面C
1A
1C与平面A
1CA夹角余弦值.
解答:
(1)证明:由题意知AA
1,AB,AC两两垂直,
建立如图所示的空间直角坐标系,
则A(0,0,0),A
1(0,0,2),B(-2,0,0),
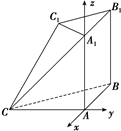
B
1 (-2,0,2),C(0,-2,0),C
1(-1,-1,2)(2分)
由
=(-1,1,2),
=(-1,-1,0),
=(-2,0,2),
设
=m
+n
,即(-2,0,2)=m(-1,-1,0)+n(-1,1,2)
即
,解得
,即
=-
+
,(4分)
即向量
、
、
共面,
又A
1C
1、CC
1在平面C
1A
1C内,AB
1不在平面C
1A
1C内,
所以AB
1∥平面C
1A
1C.(5分)
(2)解:设存在一点E,使BE⊥平面A
1CC
1,即满足
,
设
=λ
,由
=(-1,1,2),
=(2,-2,0),
得
=(2-λ,-2+λ,2λ) (6分)
又
=(-1,-1,0),所以
,解得
λ=,
所以线段CC
1上存在一点E,满足
=
,
使BE⊥平面A
1CC
1.(8分)
(3)解:设平面C
1A
1C的法向量为
=(x,y,z),
则由
,(9分)
取x=1,则y=-1,z=1.故
=(1,-1,1),
而平面A
1CA的一个法向量为
=(1,0,0),
则cos<
,
>=
=
,(11分)
平面C
1A
1C与平面A
1CA夹角余弦值为
.(12分)
点评:本题考查直线与平面平行的证明,考查直线与平面垂直的证明,考查平面与平面的夹角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.





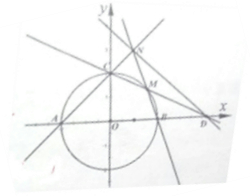 如图,圆O:x2+y2=4与坐标轴交于点A,B,C.
如图,圆O:x2+y2=4与坐标轴交于点A,B,C.