
【题目】如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD′E的位置,使得平面AD′E⊥平面ABCE.
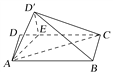
(1)求证:AE⊥BD′;
(2)求三棱锥A-BCD′的体积.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(Ⅰ)连接BD交AE于点O,推导出Rt△ABD~Rt△DAE,从而得到OB⊥AE,OD'⊥AE,由此能证明AE⊥平面OBD'.(Ⅱ)由VA﹣BCD'=VD'﹣ABC,能求出三棱锥A﹣BCD'的体积.
解析:
(1)连接BD交AE于点O,依题意得![]() ,所以Rt△ABD∽Rt△DAE,
,所以Rt△ABD∽Rt△DAE,
所以∠DAE=∠ABD,所以∠AOD=90°,所以AE⊥BD,
则OB⊥AE,OD′⊥AE,
又OB∩OD′=O,OB,OD′在平面OBD′内,
所以AE⊥平面OBD′,
又BD′平面OBD′,所以AE⊥BD′.
(2)因为平面AD′E⊥平面ABCE,
由(1)知,OD′⊥平面ABCE,
所以OD′为三棱锥D′-ABC的高,
在矩形ABCD中,AB=4,AD=2,DE=1,所以D′O=![]() ,
,
所以VA-BCD′=VD′-ABC=![]() S△ABC·D′O=
S△ABC·D′O=![]() .
.
故三棱锥A-BCD′的体积为![]() .
.


科目:高中数学 来源: 题型:
【题目】正项等差数列{an}满足a1=4,且a2,a4+2,2a7-8成等比数列,{an}的前n项和为Sn.
(1)求数列{an}的通项公式;
(2)令![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-1|.
(Ⅰ)解不等式f(x)+f(x+4)≥8;
(Ⅱ)若|a|<1,|b|<1,且a≠0,求证:f(ab)>|a|f(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856264)
已知函数f(x)=aln x,e为自然对数的底数.
(Ⅰ)曲线f(x)在点A(1,f(1))处的切线与坐标轴所围成的三角形的面积为2,求实数a的值;
(Ⅱ)若f(x)≥1-![]() 恒成立,求实数a的值取值范围.
恒成立,求实数a的值取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856289)[选修4-4:坐标系与参数方程]
直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2(sinθ+cosθ),直线l的参数方程为: ![]() (t为参数) .
(t为参数) .
(Ⅰ)写出圆C和直线l的普通方程;
(Ⅱ)点P为圆C上动点,求点P到直线l的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“扶贫帮困”是中华民族的传统美德,某校为帮扶困难同学,采用如下方式进行一次募捐:在不透明的箱子中放入大小均相同的白球七个,红球三个,每位献爱心的参与者投币20元有一次摸奖机会,一次性从箱子中摸球三个(摸完球后将球放回),若有一个红球,奖金10元,两个红球奖金20元,三个全是红球奖金100元.
(1)求献爱心参与者中将的概率;
(2)若该次募捐900位献爱心参与者,求此次募捐所得善款的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856332)
已知三棱柱ABC-A1B1C1如图所示,其中CA⊥平面ABB1A1,四边形ABB1A1为菱形,∠AA1B1=60°,E为BB1的中点,F为CB1的中点.
(Ⅰ)证明:平面AEF⊥平面CAA1C1;
(Ⅱ)若CA=2,AA1=4,求B1到平面AEF的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com