
科目:高中数学 来源: 题型:
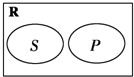 设全集为实数集R,已知非空集合S,P相互关系如图所示,其中S={x|x>10-a2},
设全集为实数集R,已知非空集合S,P相互关系如图所示,其中S={x|x>10-a2},| A、-5<a<2 | B、1<a<2 | C、1<a≤2 | D、-5≤a≤2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
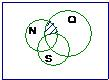 设全集I是实数集,Q={x||x|>2},N={x|
设全集I是实数集,Q={x||x|>2},N={x|| x-4 |
| x+1 |
| A、{x|4<x<5} |
| B、{x|x<2或x>3} |
| C、{x|2<x<3} |
| D、{x|2<x≤3} |
查看答案和解析>>
科目:高中数学 来源:走向清华北大同步导读·高一数学·上 题型:013
设S为全集,下面三个命题:
①若![]() ,则(
,则(![]() A)∪(
A)∪(![]() B)=S;
B)=S;
②若![]() ,则(
,则(![]() A)∩(
A)∩(![]() B)=
B)=![]() ;
;
③若![]() ,则A=B.
,则A=B.
其中假命题的个数是
[ ]
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2010年辽宁省鞍山一中高考数学六模试卷(理科)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com