
数列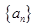 中,已知
中,已知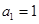 ,
,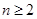 时,
时,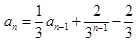 .数列
.数列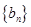 满足:
满足: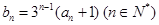 .
.
(1)证明: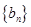 为等差数列,并求
为等差数列,并求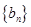 的通项公式;
的通项公式;
(2)记数列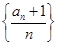 的前
的前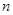 项和为
项和为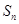 ,若不等式
,若不等式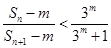 成立(
成立(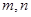 为正整数).求出所有符合条件的有序实数对
为正整数).求出所有符合条件的有序实数对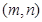 .
.
(1)通项公式 ,(2) 有序实数对
,(2) 有序实数对
【解析】
试题分析:(1)由等差数列的定义证明, 当 时,
时, 经过整理为一个常数,从而得出它的公差,进一步得出它的通项公式.
经过整理为一个常数,从而得出它的公差,进一步得出它的通项公式.
(2)利用(1)的结论, 可得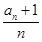 表示的式子,经判断
表示的式子,经判断 为等比数列,利用等比数列的前n项和公式求出
为等比数列,利用等比数列的前n项和公式求出 ,表示出
,表示出 为多少,利用不等式得出m的范围,进一步得出有序实数对.
为多少,利用不等式得出m的范围,进一步得出有序实数对.
试题解析:(Ⅰ) 时,
时, , 2分
, 2分
代入 整理得
整理得 ,
,
故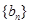 是公差为
是公差为 的等差数列. 6分
的等差数列. 6分
通项公式
(Ⅱ)由(Ⅰ)得, ,故
,故 ,所以
,所以 8分
8分
则 10分
10分
因为 ,得
,得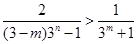 11分
11分
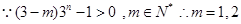 12分
12分
当 时,
时, ;当
;当 时,
时, 13分
13分
综上,存在符合条件的所有有序实数对 为:
为: . 14分
. 14分
考点:等差数列,等比数列,不等式.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com