
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时,![]() .
.

(1)已画出函数![]() 在
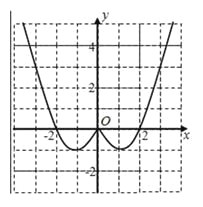
在![]() 轴左侧的图像,如图所示,请补出完整函数
轴左侧的图像,如图所示,请补出完整函数![]() 的图像,并根据图像写出函数
的图像,并根据图像写出函数![]() 的增区间;
的增区间;
⑵写出函数![]() 的解析式和值域.
的解析式和值域.
【答案】(1)函数![]() 的增区间是
的增区间是![]() ,
,![]() .
.
(2) ![]() .
.
【解析】
试题分析:(1)因为函数为偶函数,故图象关于y轴对称,由此补出完整函数f(x)的图象即可,再由图象直接可写出f(x)的增区间;(2)可由图象利用待定系数法求出x>0时的解析式,也可利用偶函数求解析式,值域可从图形直接观察得到
试题解析:(1)因为函数为偶函数,故图象关于y轴对称,补出完整函数图象如图:………3分
所以f(x)的递增区间是(﹣1,0),(1,+∞).………………5分
(2)设x>0,则﹣x<0,
所以f(﹣x)=x2﹣2x,
因为f(x)是定义在R上的偶函数,
所以f(﹣x)=f(x),
所以x>0时,f(x)=x2﹣2x,………………9分
故f(x)的解析式为 ………………10分
………………10分
值域为{y|y≥﹣1}………………12分


科目:高中数学 来源: 题型:
【题目】已知由实数组成的等比数列{an}的前项和为Sn , 且满足8a4=a7 , S7=254.
(1)求数列{an}的通项公式;
(2)对n∈N* , bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是函数y=f(x)的导函数y=f′(x)的图象,则下面判断正确的是( )
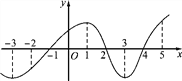
A. 在(-2,1)上f(x)是增函数 B. 在(1,3)上f(x)是减函数
C. 当x=2时,f(x)取极大值 D. 当x=4时,f(x)取极大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,如果对任意
中,如果对任意![]() 都有
都有![]() (
(![]() 为常数),则称
为常数),则称![]() 为等差比数列,
为等差比数列,![]() 称为公差比.现给出下列命题:
称为公差比.现给出下列命题:
①等差比数列的公差比一定不为![]() ;
;
②等差数列一定是等差比数列;
③若![]() ,则数列
,则数列![]() 是等差比数列;
是等差比数列;
④若等比数列是等差比数列,则其公比等于公差比.
其中正确的命题的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() “存在
“存在![]() ”,命题
”,命题![]() :“曲线
:“曲线![]() 表示焦点在
表示焦点在![]() 轴上的椭圆”,命题
轴上的椭圆”,命题![]() “曲线
“曲线![]() 表示双曲线”
表示双曲线”
(1)若“![]() 且
且![]() ”是真命题,求实数
”是真命题,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 的必要不充分条件,求实数
的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足
满足![]() ,且
,且![]() .
.
(![]() )求
)求![]() 的解析式.
的解析式.
(![]() )若函数
)若函数![]() 在区间
在区间![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围.
的取值范围.
(![]() )若
)若![]() 关于的方程
关于的方程![]() 有区间
有区间![]() 上有唯一实数根,求实数
上有唯一实数根,求实数![]() 的取值范围(相等的实数根算一个).
的取值范围(相等的实数根算一个).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)若函数![]() 的图象上的所有点的横坐标伸长到原来的
的图象上的所有点的横坐标伸长到原来的![]() 倍,所得的图象与直线
倍,所得的图象与直线![]() 交点的横坐标由小到大依次是
交点的横坐标由小到大依次是![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水产养殖基地要将一批海鲜用汽车从所在城市甲运至销售商所在城市乙,已知从城市甲到城市乙只有两条公路,且运费由水产养殖基地承担.若水产养殖基地恰能在约定日期(×月×日)将海鲜送达,则销售商一次性支付给水产养殖基地![]() 万元;若在约定日期前送到,每提前一天销售商将多支付给水产养殖基地
万元;若在约定日期前送到,每提前一天销售商将多支付给水产养殖基地![]() 万元;若在约定日期后送到,每迟到一天销售商将少支付给水产养殖基地
万元;若在约定日期后送到,每迟到一天销售商将少支付给水产养殖基地![]() 万元.为保证海鲜新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送海鲜,已知下表内的信息:
万元.为保证海鲜新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送海鲜,已知下表内的信息:
汽车 行驶路线 | 不堵车的情况下到达城市乙所需时间(天) | 堵车的情况下到达城市乙所需时间(天) | 堵车的概率 | 运费(万元) |
公路 |
|
|
|
|
公路 |
|
|
|
|
(注:毛利润![]() 销售商支付给水产养殖基地的费用
销售商支付给水产养殖基地的费用![]() 运费)
运费)
(Ⅰ)记汽车走公路![]() 时水产养殖基地获得的毛利润为
时水产养殖基地获得的毛利润为![]() (单位:万元),求
(单位:万元),求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(Ⅱ)假设你是水产养殖基地的决策者,你选择哪条公路运送海鲜有可能让水产养殖基地获得的毛利润更多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com