分析:(1)利用二项式定理对(1+
)
k和(1-
)
k展开,求出
(1+)k+(1-)k的第r+1项可以用C
kr•[(
)
k-r+(-1)
k-r•(
)
k-r]表示,对k-r分奇偶讨论,即可证明结论;
(2)根据-1<1-
<0,求出大于
(1+)2n的最小整数为
(1+)2n+(1-)2n,然后利用二项式定理展开即可证明结论.
解答:(1)证明:根据二项式定理可得:(1+
)
k的展开式的通项为T
r+1=C
kr•(
)
k-r,(1-
)
k的展开式的通项为T
r+1=C
kr•(-1)
k-r•(
)
k-r;
则
(1+)k+(1-)k的第r+1项可以用C
kr•[(
)
k-r+(-1)
k-r•(
)
k-r]表示;
当k-r为奇数时,C
kr•[(
)
k-r+(-1)
k-r•(
)
k-r]=0,当k-r为偶数时,C
kr•[(
)
k-r+(-1)
k-r•(
)
k-r]=2C
kr•(
)
k-r,是正整数,
因此
(1+)k+(1-)k是正整数;
(2)大于
(1+)2n的最小整数为
(1+)2n+(1-)2n因为-1<1-
<0,所以0<(1-
)
2n<1,
即(1+
)
2n加上此小数为一个正整数.因此大于(1+
)
2n的最小整数为
(1+)2n+(1-)2n.
记a=
,则a
2=3,由二项式展开,正负相消得
(1+
)
2n+(1-
)
2n=(1+3+2a)
n+(1+3-2a)
n=2
n[(2+a)
n+(2-a)
n]=2
n+1[2
n+2
n-23•C
n2+…]
因此能被2
n+1整除.
点评:本题是中档题.考查二项式定理的应用,同时考查了学生灵活应用知识分析解决问题的能力和运算能力.



 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案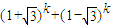 是正整数;
是正整数;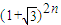 的最小整数能被2n+1整除(n∈N*)
的最小整数能被2n+1整除(n∈N*)