
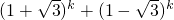 是正整数;
是正整数;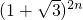 的最小整数能被2n+1整除(n∈N*)
的最小整数能被2n+1整除(n∈N*) )k的展开式的通项为Tr+1=Ckr•(
)k的展开式的通项为Tr+1=Ckr•( )k-r,(1-
)k-r,(1- )k的展开式的通项为Tr+1=Ckr•(-1)k-r•(
)k的展开式的通项为Tr+1=Ckr•(-1)k-r•( )k-r;
)k-r;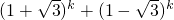 的第r+1项可以用Ckr•[(
的第r+1项可以用Ckr•[( )k-r+(-1)k-r•(
)k-r+(-1)k-r•( )k-r]表示;
)k-r]表示; )k-r+(-1)k-r•(
)k-r+(-1)k-r•( )k-r]=0,当k-r为偶数时,Ckr•[(
)k-r]=0,当k-r为偶数时,Ckr•[( )k-r+(-1)k-r•(
)k-r+(-1)k-r•( )k-r]=2Ckr•(
)k-r]=2Ckr•( )k-r,是正整数,
)k-r,是正整数,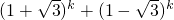 是正整数;
是正整数;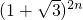 的最小整数为
的最小整数为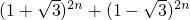
 <0,所以0<(1-
<0,所以0<(1- )2n<1,
)2n<1, )2n加上此小数为一个正整数.因此大于(1+
)2n加上此小数为一个正整数.因此大于(1+ )2n的最小整数为
)2n的最小整数为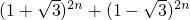 .
. ,则a2=3,由二项式展开,正负相消得
,则a2=3,由二项式展开,正负相消得 )2n+(1-
)2n+(1- )2n=(1+3+2a)n+(1+3-2a)n=2n[(2+a)n+(2-a)n]=2n+1[2n+2n-23•Cn2+…]
)2n=(1+3+2a)n+(1+3-2a)n=2n[(2+a)n+(2-a)n]=2n+1[2n+2n-23•Cn2+…] )k和(1-
)k和(1- )k展开,求出
)k展开,求出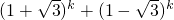 的第r+1项可以用Ckr•[(
的第r+1项可以用Ckr•[( )k-r+(-1)k-r•(
)k-r+(-1)k-r•( )k-r]表示,对k-r分奇偶讨论,即可证明结论;
)k-r]表示,对k-r分奇偶讨论,即可证明结论; <0,求出大于
<0,求出大于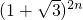 的最小整数为
的最小整数为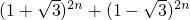 ,然后利用二项式定理展开即可证明结论.
,然后利用二项式定理展开即可证明结论.

科目:高中数学 来源:2011年江苏省苏、锡、常、镇四市高三调研数学试卷(一)(解析版) 题型:解答题
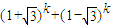 是正整数;
是正整数;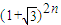 的最小整数能被2n+1整除(n∈N*)
的最小整数能被2n+1整除(n∈N*)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com