
| 停靠时间 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
| 轮船数量 | 12 | 12 | 17 | 20 | 15 | 13 | 8 | 3 |
分析 (Ⅰ)根据平均数的定义即可求出,
(Ⅱ)设出甲、乙到达的时刻,列出所有基本事件的约束条件同时列出这两艘船中至少有一艘在停靠泊位时必须等待约束条件,利用线性规划作出平面区域,利用几何概型概率公式求出概率.
解答 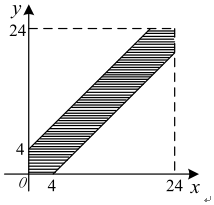 解:(Ⅰ)a=$\frac{1}{100}$(2.5×12+3×12+3.5×17+4×20+4.5×15+5×13+5.5×8+6×3)=4,
解:(Ⅰ)a=$\frac{1}{100}$(2.5×12+3×12+3.5×17+4×20+4.5×15+5×13+5.5×8+6×3)=4,
(Ⅱ)设甲船到达的时间为x,乙船到达的时间为y,则 $\left\{\begin{array}{l}{0<x<24}\\{0<y<24}\end{array}\right.$
若这两艘轮船在停靠该泊位时至少有一艘船需要等待,则|y-x|<4,
所以必须等待的概率为P=1-$\frac{2{0}^{2}}{2{4}^{2}}$=$\frac{11}{36}$,
答:这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率为$\frac{11}{36}$.
点评 本题主要考查建模、解模能力;解答关键是利用线性规划作出事件对应的平面区域,再利用几何概型概率公式求出事件的概率.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:选择题
| A. | a∧b≥2,c∧d≥2 | B. | a∧b≤2,c∨d≥2 | C. | a∨b≥2,c∧d≤2 | D. | a∨b≤2,c∨d≤2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α<β | B. | α>β | C. | α=β | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}-\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}-\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}+\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}+\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若命题p:?x0∈R,x02-x0+1<0,则¬p:?x∉R,x2-x+1≥0 | |
| B. | 命题“若x=y,则cosx=cosy”的逆否命题为真命题 | |
| C. | 已知随机变量X~N(2,σ2),若P(X<a)=0.32,则P(X>4-a)=0.68 | |
| D. | 已知相关变量(x,y)满足线性回归方程:$\stackrel{∧}{y}$=2-3x,若变量x增加一个单位,则y平均增加3个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
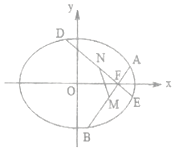 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{{\sqrt{2}}}{2}$,且过点$(\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2})$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{{\sqrt{2}}}{2}$,且过点$(\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2})$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com