Question

已知任意n个整数a₁，a₂，…，a_n，由此得到一列新的数．

由这n个数依同样法则又得到一列新数，并如此做下去．假如所有这些新数都是整数，证明原来所给各数a_i(i＝1，2，…，n)都相等．

Answer 1

证明：对于任给的n个数x_i(1≤i≤n)，如果它们不全相等，那么施行如上运算若干次后得的新数中，最大值要变小，最小值要变大，因此，如若不能得出一组n个相同的数的话，其中最大数不能永远是整数．

假设从一组n个数z₁，z₂，…，z_n得到n个相同的数

那么，当n是奇数时，易知z₁＝z₂＝…＝z_n；当n是偶数时，z₁，…，z_n中奇数项相等，偶数项相等．

若z_i(1≤i≤n)由y_i(1≤i≤n)经运算得出，且设

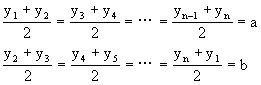
则有                                2(y₁＋y₂＋…＋y_n)＝2na

及                                2(y₂＋y₃＋…＋y_n＋y₁)＝2nb

从而                                      2na＝2nb，a＝b

由此得出z₁＝z₂＝…＝z_n＝a

因此，我们的命题成立．

仅当n为偶数时，有一种例外情况：n个整数a，b，a，b，…，a，b，(a与b的奇偶性相同，a≠b)满足题中条件，但结论不成立．