
| A£® | -$\frac{5\sqrt{3}}{9}$ | B£® | $\frac{5\sqrt{3}}{9}$ | C£® | -$\frac{\sqrt{3}}{3}$ | D£® | $\frac{\sqrt{3}}{3}$ |
·ÖÎö ÓÉÒÑÖªÀûÓÃͬ½ÇÈý½Çº¯Êý»ù±¾¹Øϵʽ¿ÉÇósin£¨$\frac{¦Ð}{4}$+¦Á£©£¬sin£¨$\frac{¦Ð}{4}$-$\frac{¦Â}{2}$£©µÄÖµ£¬ÓɦÁ+$\frac{¦Â}{2}$=£¨$\frac{¦Ð}{4}$+¦Á£©-£¨$\frac{¦Ð}{4}$-$\frac{¦Â}{2}$£©£¬ÀûÓÃÁ½½Ç²îµÄÓàÏÒº¯Êý¹«Ê½¼´¿É¼ÆËãÇóÖµµÃ½â£®
½â´ð ½â£º¡ß0£¼¦Á£¼$\frac{¦Ð}{2}$£¬cos£¨$\frac{¦Ð}{4}$+¦Á£©=$\frac{1}{3}$£¬
¡à$\frac{¦Ð}{4}$+¦Á¡Ê£¨$\frac{¦Ð}{4}$£¬$\frac{3¦Ð}{4}$£©£¬
¡àsin£¨$\frac{¦Ð}{4}$+¦Á£©=$\sqrt{1-co{s}^{2}£¨\frac{¦Ð}{4}+¦Á£©}$=$\frac{2\sqrt{2}}{3}$£¬
¡ß-¦Ð£¼¦Â£¼-$\frac{¦Ð}{2}$£¬cos£¨$\frac{¦Ð}{4}$-$\frac{¦Â}{2}$£©=-$\frac{\sqrt{3}}{3}$£¬
¡à$\frac{¦Ð}{4}$-$\frac{¦Â}{2}$¡Ê£¨$\frac{¦Ð}{2}$£¬$\frac{3¦Ð}{4}$£©£¬sin£¨$\frac{¦Ð}{4}$-$\frac{¦Â}{2}$£©=$\sqrt{1-co{s}^{2}£¨\frac{¦Ð}{4}-\frac{¦Â}{2}£©}$=$\frac{\sqrt{6}}{3}$£¬
¡àcos£¨¦Á+$\frac{¦Â}{2}$£©=cos[£¨$\frac{¦Ð}{4}$+¦Á£©-£¨$\frac{¦Ð}{4}$-$\frac{¦Â}{2}$£©]
=cos£¨$\frac{¦Ð}{4}$+¦Á£©cos£¨$\frac{¦Ð}{4}$-$\frac{¦Â}{2}$£©+sin£¨$\frac{¦Ð}{4}$+¦Á£©sin£¨$\frac{¦Ð}{4}$-$\frac{¦Â}{2}$£©
=$\frac{1}{3}¡Á$£¨-$\frac{\sqrt{3}}{3}$£©+$\frac{2\sqrt{2}}{3}$¡Á$\frac{\sqrt{6}}{3}$
=$\frac{\sqrt{3}}{3}$£®
¹ÊÑ¡£ºD£®
µãÆÀ ±¾ÌâÖ÷Òª¿¼²éÁËͬ½ÇÈý½Çº¯Êý»ù±¾¹Øϵʽ£¬Á½½Ç²îµÄÓàÏÒº¯Êý¹«Ê½ÔÚÈý½Çº¯Êý»¯¼òÇóÖµÖеÄÓ¦Ó㬿¼²éÁ˼ÆËãÄÜÁ¦ºÍת»¯Ë¼Ï룬ÊôÓÚÖеµÌ⣮



| Ä꼶 | ¸ßÖÐ¿Î³Ì | Ä꼶 | ³õÖÐ¿Î³Ì |
| ¸ßÒ» | ¸ßÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ | ³õÒ» | ³õÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ß¶þ | ¸ß¶þÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õ¶þ | ³õ¶þÃâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ßÈý | ¸ßÈýÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õÈý | ³õÈýÃâ·Ñ¿Î³ÌÍƼö£¡ |
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
| A£® | -2 | B£® | -$\frac{1}{2}$ | C£® | $\frac{1}{2}$ | D£® | 2 |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
| A£® | -$\frac{3¦Ð}{4}$ | B£® | $\frac{¦Ð}{4}$ | C£® | $\frac{7¦Ð}{4}$ | D£® | $\frac{3¦Ð}{4}$ |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
| A£® | ÍâÇÐ | B£® | Ïཻ | C£® | ÄÚÇÐ | D£® | ÏàÀë |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
| A£® | 2+i | B£® | 2-i | C£® | -1+i | D£® | -1-i |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
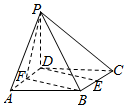 ÈçͼÒÑÖªËÄÀâ׶P-ABCDµÄµ×ÃæABCDÊDZ߳¤Îª2µÄÕý·½ÐΣ¬PD¡Íµ×ÃæABCD£¬E£¬F·Ö±ðΪÀâBC£¬ADµÄÖе㣮
ÈçͼÒÑÖªËÄÀâ׶P-ABCDµÄµ×ÃæABCDÊDZ߳¤Îª2µÄÕý·½ÐΣ¬PD¡Íµ×ÃæABCD£¬E£¬F·Ö±ðΪÀâBC£¬ADµÄÖе㣮²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
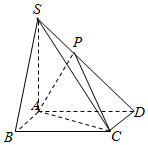 Èçͼ£¬ÔÚËÄÀâ׶S-ABCDÖУ¬µ×ÃæABCDΪ¾ØÐΣ¬SA¡ÍƽÃæABCD£¬AB=1£¬AD=AS=2£¬PÊÇÀâSDÉÏÒ»µã£¬ÇÒ$SP=\frac{1}{2}PD$£®
Èçͼ£¬ÔÚËÄÀâ׶S-ABCDÖУ¬µ×ÃæABCDΪ¾ØÐΣ¬SA¡ÍƽÃæABCD£¬AB=1£¬AD=AS=2£¬PÊÇÀâSDÉÏÒ»µã£¬ÇÒ$SP=\frac{1}{2}PD$£®²é¿´´ð°¸ºÍ½âÎö>>
¹ú¼ÊѧУÓÅÑ¡ - Á·Ï°²áÁбí - ÊÔÌâÁбí
ºþ±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨Æ½Ì¨ | ÍøÉÏÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | µçÐÅթƾٱ¨×¨Çø | ÉæÀúÊ·ÐéÎÞÖ÷ÒåÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com