
【题目】已知数列![]() 的首项为1.记
的首项为1.记![]() .
.
(1)若![]() 为常数列,求
为常数列,求![]() 的值:
的值:
(2)若![]() 为公比为2的等比数列,求
为公比为2的等比数列,求![]() 的解析式:
的解析式:
(3)是否存在等差数列![]() ,使得
,使得![]() 对一切
对一切![]() 都成立?若存在,求出数列
都成立?若存在,求出数列![]() 的通项公式:若不存在,请说明理由.
的通项公式:若不存在,请说明理由.
 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:
【题目】旅游业作为一个第三产业,时间性和季节性非常强,每年11月份来临,全国各地就相继进入旅游淡季,很多旅游景区就变得门庭冷落.为改变这种局面,某旅游公司借助一自媒体平台做宣传推广,销售特惠旅游产品.该公司统计了活动刚推出一周内产品的销售数量,用![]() 表示活动推出的天数,用
表示活动推出的天数,用![]() 表示产品的销售数量(单位:百件),统计数据如下表所示.
表示产品的销售数量(单位:百件),统计数据如下表所示.
![]()

根据以上数据,绘制了如图所示的散点图,根据已有的函数知识,发现样本点分布在某一条指数型函数![]() 的周围.为求出该回归方程,相关人员确定的研究方案是:先用其中5个数据建立
的周围.为求出该回归方程,相关人员确定的研究方案是:先用其中5个数据建立![]() 关于
关于![]() 的回归方程,再用剩下的2组数据进行检验.试回答下列问题:
的回归方程,再用剩下的2组数据进行检验.试回答下列问题:
(1)现令![]() ,若选取的是
,若选取的是![]() 这5组数据,已知
这5组数据,已知![]() ,
,![]() ,请求出
,请求出![]() 关于
关于![]() 的线性回归方程(结果保留一位有效数字);
的线性回归方程(结果保留一位有效数字);
(2)若由回归方程得到的估计数据与选出的检验数据的误差均不超过![]() ,则认为得到的回归方程是可靠的,试问(1)中所得的回归方程是否可靠?
,则认为得到的回归方程是可靠的,试问(1)中所得的回归方程是否可靠?
参考公式及数据:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为 ,
, ![]() ;
;![]() ;
;![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() :
:![]() 的一个顶点重合,且这个顶点与椭圆
的一个顶点重合,且这个顶点与椭圆![]() 的两个焦点构成的三角形面积为
的两个焦点构成的三角形面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若椭圆![]() 的上顶点为
的上顶点为![]() ,过
,过![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点,连接
为坐标原点,连接![]() 并延长交椭圆于点
并延长交椭圆于点![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1).在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图(2).
,如图(2).

(1)求证:![]() 平面
平面![]() ;
;
(2)当点![]() 在何处时,三棱锥
在何处时,三棱锥![]() 体积最大,并求出最大值;
体积最大,并求出最大值;
(3)当三棱锥![]() 体积最大时,求
体积最大时,求![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为提升学生的数学学习能力,进行了主题分别为“运算”、“推理”、“想象”、“建模”四场竞赛.规定:每场竞赛前三名得分分别为![]() 、
、![]() 、
、![]() (
(![]() ,且
,且![]() 、
、![]() 、
、![]() ),选手的最终得分为各场得分之和.最终甲、乙、丙三人包揽了每场竞赛的前三名,在四场竞赛中,已知甲最终得分为
),选手的最终得分为各场得分之和.最终甲、乙、丙三人包揽了每场竞赛的前三名,在四场竞赛中,已知甲最终得分为![]() 分,乙最终得分为
分,乙最终得分为![]() 分,丙最终得分为
分,丙最终得分为![]() 分,且乙在“运算”这场竞赛中获得了第一名,那么“运算”这场竞赛的第三名是( )
分,且乙在“运算”这场竞赛中获得了第一名,那么“运算”这场竞赛的第三名是( )
A.甲B.乙C.丙D.甲和丙都有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某市高三数学复习备考情况,该市教研机构组织了一次检测考试,并随机抽取了部分高三理科学生数学成绩绘制如图所示的频率分布直方图.

(1)根据频率分布直方图,估计该市此次检测理科数学的平均成绩![]() ;(精确到个位)
;(精确到个位)
(2)研究发现,本次检测的理科数学成绩![]() 近似服从正态分布
近似服从正态分布![]() (
(![]() ,
,![]() 约为
约为![]() ),按以往的统计数据,理科数学成绩能达到自主招生分数要求的同学约占
),按以往的统计数据,理科数学成绩能达到自主招生分数要求的同学约占![]() .
.
(ⅰ)估计本次检测成绩达到自主招生分数要求的理科数学成绩大约是多少分?(精确到个位)
(ⅱ)从该市高三理科学生中随机抽取![]() 人,记理科数学成绩能达到自主招生分数要求的人数为
人,记理科数学成绩能达到自主招生分数要求的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .(说明:
.(说明:![]() 表示
表示![]() 的概率.参考数据:
的概率.参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
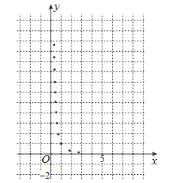
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若旋转的弧度数![]() 与单位时间内煤气输出量
与单位时间内煤气输出量![]() 成正比,那么
成正比,那么![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为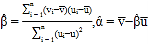 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com