
(本题满分12分)设二次函数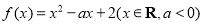 ,关于
,关于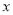 的不等式
的不等式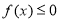 的解集有且只有一个元素.
的解集有且只有一个元素.
(1)设数列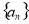 的前
的前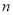 项和
项和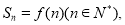 求数列
求数列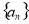 的通项公式;
的通项公式;
(2)记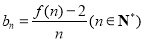 ,求数列
,求数列 中是否存在不同的三项能组成等比数列?请说明理由.
中是否存在不同的三项能组成等比数列?请说明理由.
(1)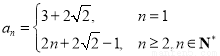 (2)数列
(2)数列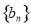 中不存在不同的三项能组成等
中不存在不同的三项能组成等
比数列
【解析】
试题分析:第(1)问由不等式 的解集有且只有一个元素,得到
的解集有且只有一个元素,得到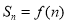 ,然后由此求出数列
,然后由此求出数列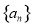 的通项公式,由
的通项公式,由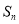 求通项
求通项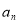 时注意检验初始项
时注意检验初始项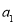 是否满足;第(2)问判断数列
是否满足;第(2)问判断数列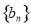 中是否存在不同的三项能组成等比数列,基本方法是先假设它们成等比数列,再证明问题是否有解.
中是否存在不同的三项能组成等比数列,基本方法是先假设它们成等比数列,再证明问题是否有解.
试题解析:(1)因为关于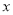 的不等式
的不等式 的解集有且只有一个元素,
的解集有且只有一个元素,
所以二次函数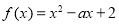 (
(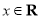 )的图象与
)的图象与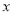 轴相切,
轴相切,
则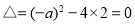 ,考虑到
,考虑到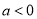 ,所以
,所以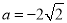 .
.
从而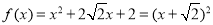 ,
,
所以数列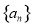 的前
的前 项和
项和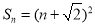 (
(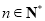 ).
).
于是当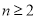 ,
,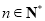 时,
时,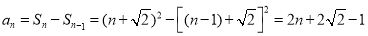 ,
,
当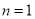 时,
时,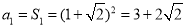 ,不适合上式.
,不适合上式.
所以数列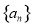 的通项公式为
的通项公式为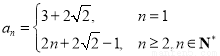 .
.
(2)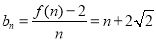 .
.
假设数列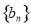 中存在三项
中存在三项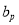 ,
,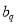 ,
,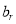 (正整数
(正整数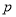 ,
,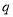 ,
,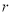 互不相等)成等比数列,则
互不相等)成等比数列,则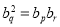 ,
,
即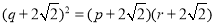 ,整理得
,整理得 .
.
因为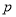 ,
,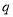 ,
,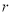 都是正整数,所以
都是正整数,所以 ,
,
于是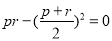 ,即
,即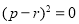 ,从而
,从而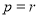 与
与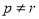 矛盾.
矛盾.
故数列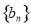 中不存在不同的三项能组成等比数列.
中不存在不同的三项能组成等比数列.
考点:数列通项公式,等比数列性质.


科目:高中数学 来源:2014-2015学年稳派新课程高三2月精品理科数学试卷(解析版) 题型:填空题
我国齐梁时代的数学家祖暅(公元前5-6世纪)提出了一条原理“幂势既同,则积不容异.”
这句话的意思是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任何平面所截,如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等.设由曲线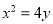 和直线
和直线 所围成的平面图形,绕
所围成的平面图形,绕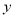 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为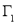 ;由同时满足
;由同时满足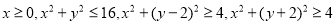 的点
的点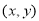 构成的平面图形,绕
构成的平面图形,绕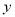 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为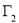 ;根据祖暅原理等知识,通过考察
;根据祖暅原理等知识,通过考察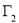 可以得到
可以得到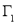 的体积为 .
的体积为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年稳派新课程高三2月精品理科数学试卷(解析版) 题型:选择题
在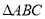 中,内角
中,内角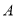 ,
,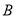 ,
,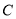 所对应的边分别为
所对应的边分别为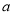 ,
,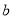 ,
,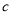 ,若
,若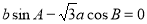 ,且
,且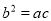 ,则
,则 的值为( )
的值为( )
A.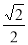 B.
B. C.2 D.4
C.2 D.4
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市长宁区高三上学期教学质量检测文科数学试卷(解析版) 题型:填空题
已知△ABC中,角A、B、C的对边分别为a、b、c,且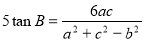 , 则
, 则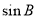 的值是 .
的值是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年陕西省高三教学质量检测一文科数学试卷(解析版) 题型:选择题
已知直线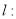
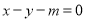 经过抛物线
经过抛物线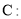
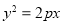 (
(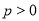 )的焦点,
)的焦点,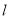 与
与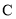 交于
交于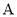 、
、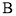 两点.若
两点.若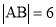 ,则
,则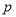 的值为( )
的值为( )
A.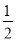 B.
B.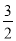 C.
C.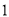 D.
D.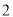
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com