
【题目】在边长为4的菱形ABCD中,∠DAB=60°,点E,F分别是边CD,CB的中点,AC∩EF=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图的五棱锥,且 ![]() .
. 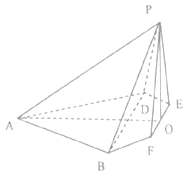
(1)求证:BD⊥平面POA;
(2)求二面角B﹣AP﹣O的余弦值.
【答案】
(1)证明:∵点E,F分别为CD,CB的中点,∴BD∥EF,
∵菱形ABCD的对角线互相垂直,
∴BD⊥AC,∴EF⊥AC,∴EF⊥AO,EF⊥PO,
∵AO平面POA,PO平面POA,AO∩PO=O,
∴EF⊥平面POA,∴BD⊥平面POA.
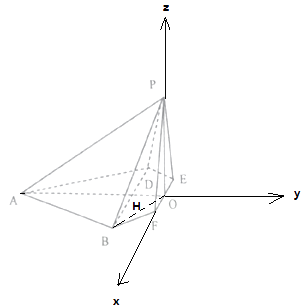
(2)解:设AO∩BD=H,连接BO,∵∠DAB=60°,∴△ABD为等边三角形,
∴ ![]() ,
,
在Rt△BHO中, ![]() ,
,
在△PBO中,BO2+PO2=10=PB2,∴PO⊥BO,
∵PO⊥EF,EF∩BO=O,EF平面BFED,∴PO⊥平面BFED,
以O为原点,OF所在直线为x轴,AO所在直线y轴,OP所在直线为z轴,建立空间直角坐标系O﹣xyz,
则 ![]() .
.
∴ ![]() ,
,
设平面PAB的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 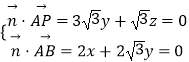 ,取y=1,得
,取y=1,得 ![]() =(﹣
=(﹣ ![]() ),
),
∵BD⊥平面POA,AO∩BD=H,∴平面PAO的一个法向量为 ![]() =(﹣2,0,0),
=(﹣2,0,0),
设二面角B﹣AP﹣O的平面角为θ,
则cosθ= 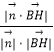 =
= ![]() =
= ![]() ,
,
∴二面角B﹣AP﹣O的余弦值为 ![]() .
.
【解析】(1)推导出BD∥EF,BD⊥AC,EF⊥AC,从而EF⊥AO,EF⊥PO,由此能证明BD⊥平面POA.(2)设AO∩BD=H,连接BO,以O为原点,OF所在直线为x轴,AO所在直线y轴,OP所在直线为z轴,建立空间直角坐标系O﹣xyz,利用向量法能求出二面角B﹣AP﹣O的余弦值.
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】我国古代有着辉煌的数学研究成果.《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、…、《辑古算经》等算经10部专著,有着十分丰富多彩的内容,是了解我国古代数学的重要文献.这10部专著中有7部产生于魏晋南北朝时期.某中学拟从这10部名著中选择2部作为“数学文化”校本课程学习内容,则所选2部名著中至少有一部是魏晋南北朝时期的名著的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖冲之之子祖暅是我国南北朝时代伟大的科学家,他在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”.意思是,如果两个等高的几何体 在同高处截得的截面面积恒等,那么这两个几何体的体积相等.此即祖暅原理.利用这个原理求球的体积时,需要构造一个满足条件的几何体,已知该几何体三视图 如图所示,用一个与该几何体的下底面平行相距为 h(0<h<2) 的平面截该几何体,则截面面积为 ( )

A.![]()
B.![]()
C.![]()
D.π(4-h2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(x)+f(x﹣1)=0,且在[﹣5,﹣4]上是增函数,A,B是锐角三角形的两个内角,则( )
A.f(sinA)>f(cosB)
B.f(sinA)<f(cosB)
C.f(sinA)>f(sinB)
D.f(cosA)>f(cosB)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统综》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔仔细算相还”.其大意为:“有一个走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地”.则该人第五天走的路程为( )
A.48里
B.24里
C.12里
D.6里
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】传统文化就是文明演化而汇集成的一种反映民族特质和风貌的民族文化,是民族历史上各种思想文化、观念形态的总体表征.教育部考试中心确定了2017年普通高考部分学科更注重传统文化考核.某校为了了解高二年级中国数学传统文化选修课的教学效果,进行了一次阶段检测,并从中随机抽取80名同学的成绩,然后就其成绩分为A、B、C、D、E五个等级进行数据统计如下:
成绩 | 人数 |
A | 9 |
B | 12 |
C | 31 |
D | 22 |
E | 6 |
根据以上抽样调查数据,视频率为概率.
(1)若该校高二年级共有1000名学生,试估算该校高二年级学生获得成绩为B的人数;
(2)若等级A、B、C、D、E分别对应100分、80分、60分、40分、20分,学校要求“平均分达60分以上”为“教学达标”,请问该校高二年级此阶段教学是否达标?
(3)为更深入了解教学情况,将成绩等级为A、B的学生中,按分层抽样抽取7人,再从中任意抽取3名,求抽到成绩为A的人数X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )图象如图所示,则下列关于函数 f (x)的说法中正确的是( )
)图象如图所示,则下列关于函数 f (x)的说法中正确的是( ) 
A.对称轴方程是x= ![]() +kπ(k∈Z)
+kπ(k∈Z)
B.对称中心坐标是( ![]() +kπ,0)(k∈Z)
+kπ,0)(k∈Z)
C.在区间(﹣ ![]() ,
, ![]() )上单调递增
)上单调递增
D.在区间(﹣π,﹣ ![]() )上单调递减
)上单调递减
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com