
【题目】定义在R上的偶函数f(x)满足f(x)+f(x﹣1)=0,且在[﹣5,﹣4]上是增函数,A,B是锐角三角形的两个内角,则( )
A.f(sinA)>f(cosB)
B.f(sinA)<f(cosB)
C.f(sinA)>f(sinB)
D.f(cosA)>f(cosB)
【答案】B
【解析】解:∵A、B是锐角三角形的两个内角, ∴A+B> ![]() ,可得A>
,可得A> ![]() ﹣B,
﹣B,
∵y=cosx在区间(0, ![]() )上是减函数,
)上是减函数, ![]() >A>
>A> ![]() ﹣B>0,
﹣B>0,
∴sinA>sin( ![]() ﹣B)=cosB,即锐角三角形的两个内角A、B是满足sinA>cosB,
﹣B)=cosB,即锐角三角形的两个内角A、B是满足sinA>cosB,
∵函数f(x)满足f(x+1)=﹣f(x),
∴f(x+2)=﹣f(x+1)=﹣[﹣f(x)]=f(x),可得函数f(x)是周期为2的函数.
∵f(x)在[﹣5,﹣4]上是增函数,
∴f(x)在[﹣1,0]上也是增函数,
再结合函数f(x)是定义在R上的偶函数,可得f(x)在[0,1]上是减函数.
∵锐角三角形的两个内角A、B是满足sinA>cosB,且sinB、cosA∈[0,1]
∴f(sinA)<f(cosB).
故选:B


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,x轴为极轴建立极坐标系,曲线C1的方程为 ![]() (θ为参数),曲线C2的极坐标方程为C2:ρcosθ+ρsinθ=1,若曲线C1与C2相交于A、B两点.
(θ为参数),曲线C2的极坐标方程为C2:ρcosθ+ρsinθ=1,若曲线C1与C2相交于A、B两点.
(1)求|AB|的值;
(2)求点M(﹣1,2)到A、B两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如图所示的程序框图,则该算法的功能是( ) 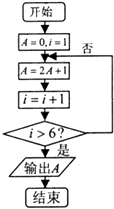
A.计算数列{2n﹣1}前5项的和
B.计算数列{2n﹣1}前5项的和
C.计算数列{2n﹣1}前6项的和
D.计算数列{2n﹣1}前6项的和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列{an}中,a1=3,其前n项和为Sn , 等比数列{bn}的各项均为正数,b1=1,公比为q,且b2+S2=12,q= ![]() (Ⅰ)求an与bn;
(Ⅰ)求an与bn;
(Ⅱ)设数列{cn}满足cn= ![]() ,求{cn}的前n项和Tn .
,求{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在矩阵A的变换下,坐标平面上的点的横坐标伸长到原来的3倍,纵坐标不变.
(1)求矩阵A及A﹣1;
(2)求圆x2+y2=4在矩阵A﹣1的变换下得到的曲线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为4的菱形ABCD中,∠DAB=60°,点E,F分别是边CD,CB的中点,AC∩EF=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图的五棱锥,且 ![]() .
. 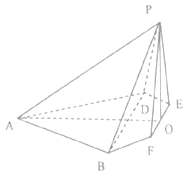
(1)求证:BD⊥平面POA;
(2)求二面角B﹣AP﹣O的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解该校高三年级学生数学科学习情况,对广一模考试数学成绩进行分析,从中抽取了n 名学生的成绩作为样本进行统计(该校全体学生的成绩均在[60,140),按照[60,70),[70,80),[80,90),[90,100),[100,110),[110,120),[120,130),[130,140)的分组作出频率分布直方图如图1所示,样本中分数在[70,90)内的所有数据的茎叶图如图2所示. 
根据上级统计划出预录分数线,有下列分数与可能被录取院校层次对照表为表( c ).
分数 | [50,85] | [85,110] | [110,150] |
可能被录取院校层次 | 专科 | 本科 | 重本 |
(1)求n和频率分布直方图中的x,y的值;
(2)根据样本估计总体的思想,以事件发生的频率作为概率,若在该校高三年级学生中任取3 人,求至少有一人是可能录取为重本层次院校的概率;
(3)在选取的样本中,从可能录取为重本和专科两个层次的学生中随机抽取3 名学生进行调研,用ξ表示所抽取的3 名学生中为重本的人数,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com