
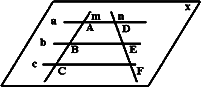
直线m、n分别和平行直线a、b、c都相交,交点为A、B、C、D、E、F,如图,求证:直线a、b、c、m、n共面.
 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
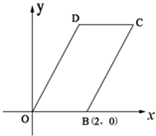
 如图所示,四边形OABP是平行四边形,过点P的直线与射线OA、OB分别相交于点M、N,若
如图所示,四边形OABP是平行四边形,过点P的直线与射线OA、OB分别相交于点M、N,若 | OM |
| OA |
| ON |
| OB |
| NM |
| MP |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知四边形OBCD是平行四边形,|OB|=2,|OD|=4,∠DOB=60°,直线x=t(0<t<4)分别交平行四边行两边于不同的两点M、N.
如图,已知四边形OBCD是平行四边形,|OB|=2,|OD|=4,∠DOB=60°,直线x=t(0<t<4)分别交平行四边行两边于不同的两点M、N.查看答案和解析>>
科目:高中数学 来源:学习周报 数学 人教课标高一版(A必修2) 2009-2010学年 第17期 总173期 人教课标高一版 题型:044
如图,在矩形ABCD和矩形ABEF中,矩形ABEF可沿AB任意翻折,AF=AD,点M,N分别在AE,DB上运动,且满足AM=DN.
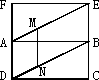
(1)当F,A,D三点不共线,且M,N分别不与A,D重合时,试判断MN与平面FAD是否平行;
(2)在翻折矩形ABEF的过程中,试判断直线MN与FD的位置关系.
查看答案和解析>>
科目:高中数学 来源:选修设计数学A4-1人教版 人教版 题型:022
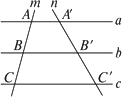
用符号语言表述是:已知a∥b∥c,直线m、n分别与a、b、c交于点A、B、C和![]() 、
、![]() 、
、![]() (如图),如果________,那么________.
(如图),如果________,那么________.
对于定理的证明,分m平行于n和m不平行于n两种情况证明.当m平行于n时,直接运用平行四边形加以证明;当m不平行于n时,利用辅助线构造相似三角形,进而关系式得证.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com