练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （13分）已知圆M: 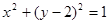,Q是x轴上的动点，QA、QB分别切圆M于A、B两点。

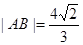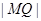    (1)若，求的长；

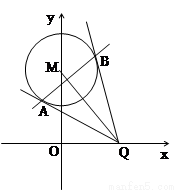    (2)求证：直线AB恒过定点，并求出定点坐标．

     

     

     

     

     

     

     

     

     

    【答案】

    （1）

    （2）直线AB：，直线AB过定点（0，）

    【解析】（1）由，

    ∴……3分

        Rt△MBQ中，由|MB|2=|MP|MQ|得|MQ|=3……6分

    （2）设Q（，0），∵M（0，2）

    则以MQ为直径的圆的方程： ……8分

     由，两式相减得直线AB：……11分

     即直线AB： ∴直线AB过定点（0，）……13分

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知圆M：（x-m）2+（y-n）2=γ2及定点N（1，0），点P是圆M上的动点，点Q在NP上，点G在MP上，且满足
    NP
    =2
    NQ
    ，
    GQ
    •
    NP
    =0．
    （Ⅰ）若m=-1，n=0，r=4，求点G的轨迹C的方程；
    （Ⅱ）若动圆M和（Ⅰ）中所求轨迹C相交于不同两点A、B，是否存在一组正实数m，n，r使得直线MN垂直平分线段AB，若存在，求出这组正实数；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知圆M：（x+cosq）2+（y-sinq）2=1，直线l：y=kx，下面四个命题：
    （A）对任意实数k与q，直线l和圆M相切；
    （B）对任意实数k与q，直线l和圆M有公共点；
    （C）对任意实数q，必存在实数k，使得直线l与和圆M相切
    （D）对任意实数k，必存在实数q，使得直线l与和圆M相切
    其中真命题的代号是
     
    ．（写出所有真命题的代号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，已知圆M：（x+1）2+y2=8及定点N（1，0），点P是圆M上一动点，点Q为PN的中点，PM上一点G满足
    GQ
    •
    NP
    =0
    （1）求点G的轨迹C的方程；
    （2）已知直线l：y=kx+m与曲线C交于A、B两点，E（0，1），是否存在直线l，使得点N恰为△ABE的垂心？若存在，求出直线l的方程，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2014届四川省高二10月月考文科数学试卷（解析版） 题型：填空题

    已知圆M：（x＋cosq）2＋（y－sinq）2＝1，直线l：y＝kx，下面四个命题

    ①对任意实数k与q，直线l和圆M相切；

    ②对任意实数k与q，直线l和圆M有公共点；

    ③对任意实数q，必存在实数k，使得直线l与和圆M相切;

    ④对任意实数k，必存在实数q，使得直线l与和圆M相切.

    其中真命题的代号是______________（写出所有真命题的代号）.

     

    查看答案和解析>>

    同步练习册答案