Question

如图，在直三棱柱ABC—A₁B₁C₁中，底面是等腰直角三角形，∠ACB=90°，侧棱AA₁=2，D、E分别是CC₁与A₁B的中点，点E在平面ABD上的射影是△ABD的重心G.

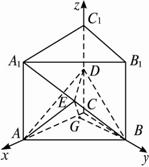
（1）求A₁B与平面ABD所成角的大小；

（2）求点A₁到平面AED的距离.

Answer 1

解析：由于题目中给出直三棱柱及∠ACB=90°,从而可以判断AC、BC、CC₁三直线两两互相垂直，由此可以考虑建立空间直角坐标系，将两个问题都转化到向量的有关计算中去，也可以用自由向量求解，第（2）题还可以利用函数的最值来求解.?

（1）方法一：建立如图所示的空间直角坐标系，原点为C点，设CA=2a，则C（0，0，0），A（2a,0,0）,B(0,2a,0),?D(0,0，1)?,A₁(2a,0,2),E(a,a,1),G(,,),?

∴=(,,),=(0,-2a,1).?

∵EG⊥面ABD，∴·=0.?

∴-a²+=0，即a=1.?

∴=（2，-2，2），=（，-，）.?

∴·=，||=2，||=.?

∵GE⊥平面ABD，∴BG是BE在面ABD上的射影，即∠A₁BG是A₁B与平面ABD所成的角.

∴cos∠A₁BG=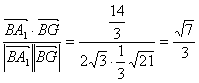，A₁B与平面ABD所成角是arccos.?

方法二：（法向量法）（接方法一）设平面ABD的法向量为n=(λ,u,1),?

∵=(-2a,0,1),=(0,-2a,1),n⊥平面ABD，∴n·=0，n·=0.?

∴-2λa+1=0.∴-2ua+1=0.?

∴λ=u=.∴n=(,,1).?

又∵=(,,)，而EG⊥平面ABD，?

∴·=0.∴-a²+=0.?

∴a=1.∴n=(,,1), =(-2,2,-2).?

∴n与的夹角为〈n, 〉.?

∴cos〈n, 〉=.?

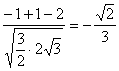设A₁B与平面ABD所成角为θ，?

∴sinθ=|cos〈n, 〉|=,cosθ=.?

∴θ=arcsin=arccos.?

方法三：（自由向量法）设=a，=b， =c，?

∴=b-a， =-=b-a-c， =a+c-b，，（a+c-2b）.?

∴?

=（a+b+2c）.?

又∵GE⊥面ABD，∴GE·BD=0.?

∴（a+b+2c）·（c-2b）=0.?

∴a·c+b·c+2c-2a·b-2b²-4b·c=0.?

∵a,b,c两两垂直，∴a·b=b·c=c·a=0.?

∴b²=c².∴|b|=|c|.∵|c|=2,∴|a|=|b|=2.?

∵=(a+c-b)·（2a+c-4b）=（c²+4b²+2a²）=|c|²=,?

又||²=（a+c-b）²=（a²+c²+b²）?

=|a|²=3，?

∴||=.?

又||=（2a+c-4b）²=（4a²+c²+16b²）?

=|a|²=，?

∴||=.?

∵GE⊥平面ABD，

∴BG是BE在面ABD上的射影.?

∴∠GBE是A₁B与面ABD所成的角.?

∴cos∠GBE=.?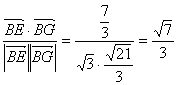

∴∠GBE=arccos.?

（2）方法一：由（1）的方法一有A（2，0，0），A₁（2，0，2），E（1，1，1），D（0，0，1）.?

=（-1，1，1）·（-1，-1，0）=0， =（0，0，2）·（-1，-1，0）=0，∴ED⊥平面AA₁E.?

又∵ED平面AED，?

∴平面AED⊥平面AA₁E，交线为AE.?

∴点A₁在平面AED上的射影K在AE上.?

设=λ，则=（-λ,λ,λ-2），?

由 =0，即λ+λ+λ-2=0,∴λ=.?

∴=(-,,-).

∴||=.?

故A₁到平面AED的距离为.?

方法二：（法向量法）设平面ADE的法向量为?

n=（x,y,1），且=（-2，0，1），=（1，1，0），=（0，0，2）.?

故有n·=0，n·=0，即?

解之，得∴n=(0.5,-0.5,1).?

设A₁点到平面AED的距离为d，则?

d=.?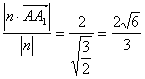

方法三：（自由向量法）由（1）的方法三知?

|a|=|b|=|c|=2，?

，?

.?

设点M∈面AED，?

∴=x+y=［(x-y)a+(-x-y)b-xc］，?

∴??

=［(x-y)a+(-x-y)b-xc］+ (b-c-a)?

=［(x-y-1)a+(-x-y+1)b-(x+1)c］.?

∵a·b=b·c=c·a=0，?

∴||²=［(x-y-1)a-(x+y-1)b-(x+1)c］²?

=［(x-y-1)²a²+(x+y-1)²b²+(x+1)²c²］?

=［(x-y-1)²+(x+y-1)²+(x+1)²］a²?

=2(x-1)²-2(x-1)y+2(x-1)y+y²+(x+1)²?

=3x²-2x+y²+3?

=3(x-)²+y²+.?

∴当且仅当x=，且y=0时，||²有最小值.?

∴||=.

∴点A₁到平面AED的距离为.