Question

设0≤x≤2，则函数y=2^2x-1-3×2^x+5的最大值是________．

Answer 1

分析：由0≤x≤2，知1≤2^x≤4，再由y=2^2x-1-3×2^x+5=×（2^x-3）²+，能求出函数y=2^2x-1-3×2^x+5的最大值．
解答：∵0≤x≤2，∴1≤2^x≤4，
∴y=2^2x-1-3×2^x+5
=×（2^x）²-3×2^x+5
=×（2^x-3）²+，
∴当2^x=1时，函数y=2^2x-1-3×2^x+5的最大值==．
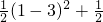
故答案为：．
点评：本题考查函数的最大值的求法，解题时要认真审题，注意配方法的合理运用．