
 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.科目:高中数学 来源:不详 题型:解答题
 ,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为
,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为 米与
米与 米均不小于2米,且要求“转角处”(图中矩形
米均不小于2米,且要求“转角处”(图中矩形 )的面积为8平方米
)的面积为8平方米 表示草坪的面积
表示草坪的面积 ,并指出
,并指出 的取值范围
的取值范围 、
、 ,才能使草坪的面积最大?并求出草坪的最大面积。
,才能使草坪的面积最大?并求出草坪的最大面积。
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 城周边已有两条公路
城周边已有两条公路 在点O处交汇,且它们的夹角为
在点O处交汇,且它们的夹角为 .已知
.已知 ,
,  与公路
与公路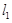 夹角为
夹角为 .现规划在公路
.现规划在公路 上分别选择
上分别选择 两处作为交汇点(异于点O)直接修建一条公路通过
两处作为交汇点(异于点O)直接修建一条公路通过 城.设
城.设
 ,
,
 .
. 关于
关于 的函数关系式并指出它的定义域;
的函数关系式并指出它的定义域; 的面积最小.
的面积最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com