【答案】
分析:(1)根据y=
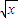
与圆C
n交于点N,可得
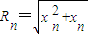
,确定直线MN的方程,利用点N(x
n,y
n)在直线MN上,即可用x
n表示R
n和a
n;
(2)由x
n+1=4x
n+3得{x
n+1}是以4为首项,4为公比的等比数列,由此可求
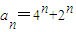
,①利用数列{a
n+1-p•a
n}成等比数列,构建等式,即可求得结论;
②由①知:
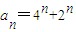
,构建函数f(x)=(x+1)
n-x
n(x>0),证明函数是增函数,即可得到结论.
解答:解:(1)∵y=

与圆C
n交于点N,∴
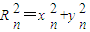
=
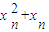
∴
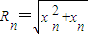
,…(2分)
由题可知,点M的坐标为(0,R
n),从而直线MN的方程为
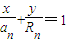
,…(3分)
由点N(x
n,y
n)在直线MN上得:
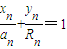
,…(4分)
将
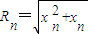
,

代入化简得:
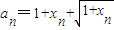
.…(6分)
(2)由x
n+1=4x
n+3得:1+x
n+1=4(x
n+1),…(7分)
又x
1=3,∴1+x
1=4,故{x
n+1}是以4为首项,4为公比的等比数列
∴x
n+1=4•4
n-1=4
n,∴
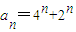
…(8分)
①a
n+1-p•a
n=4
n+1+2
n+1-p(4
n+2
n)=(4-p)•4
n+(2-p)•2
n,a
n+2-p•a
n+1=(16-4p)•4
n+(4-2p)•2
n令a
n+2-p•a
n+1=q(a
n+1-p•a
n)得:(16-4p)•4
n+(4-2p)•2
n=q[(4-p)•4
n+(2-p)•2
n]…(9分)
∴
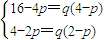
,∴
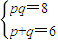
,解得:
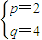
或
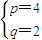
故当p=2时,数列{a
n+1-p•a
n}成公比为4的等比数列;当p=4时,数列{a
n+1-p•a
n}成公比为2的等比数列. …(11分)
②由①知:
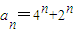
,当n=1时,
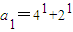
=3•2
1;
当n≥2时,
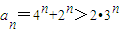
.…(12分)
事实上,令f(x)=(x+1)
n-x
n(x>0),则f′(x)=n[(x+1)
n-1-x
n-1]>0,
故f(x)=(x+1)
n-x
n(x>0)是增函数,
∴f(3)>f(2),即:4
n-3
n>3
n-2
n,即
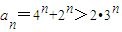
.…(14分)
点评:本题考查数列与函数的综合,考查数列的通项,考查大小比较,确定数列的通项是关键,属于中档题.

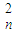 (Rn>0)与y轴正半轴的交点为M,与曲线y=
(Rn>0)与y轴正半轴的交点为M,与曲线y=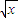 的交点为N(xn,yn),直线MN与x轴的交点为A(an,0).
的交点为N(xn,yn),直线MN与x轴的交点为A(an,0).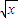 与圆Cn交于点N,可得
与圆Cn交于点N,可得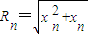 ,确定直线MN的方程,利用点N(xn,yn)在直线MN上,即可用xn表示Rn和an;
,确定直线MN的方程,利用点N(xn,yn)在直线MN上,即可用xn表示Rn和an;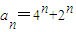 ,①利用数列{an+1-p•an}成等比数列,构建等式,即可求得结论;
,①利用数列{an+1-p•an}成等比数列,构建等式,即可求得结论;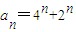 ,构建函数f(x)=(x+1)n-xn(x>0),证明函数是增函数,即可得到结论.
,构建函数f(x)=(x+1)n-xn(x>0),证明函数是增函数,即可得到结论. 与圆Cn交于点N,∴
与圆Cn交于点N,∴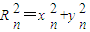 =
=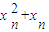
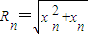 ,…(2分)
,…(2分)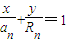 ,…(3分)
,…(3分)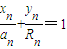 ,…(4分)
,…(4分)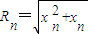 ,
, 代入化简得:
代入化简得: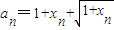 .…(6分)
.…(6分)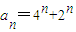 …(8分)
…(8分)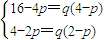 ,∴
,∴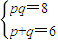 ,解得:
,解得: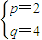 或
或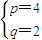
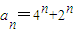 ,当n=1时,
,当n=1时,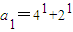 =3•21;
=3•21;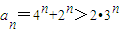 .…(12分)
.…(12分)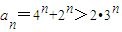 .…(14分)
.…(14分)

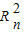 (Rn>0)与y轴正半轴的交点为M,与曲线
(Rn>0)与y轴正半轴的交点为M,与曲线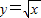 的交点为N(
的交点为N(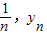 ),直线MN与x轴的交点为A(an,0).
),直线MN与x轴的交点为A(an,0). ,求证:
,求证: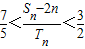 .
.