
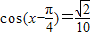 ,
,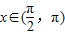 .
.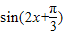 的值.
的值.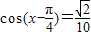 ,
,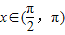 .
.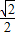 (sinx+cosx)=
(sinx+cosx)=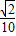 ;
; ⇒cosx=
⇒cosx= -sinx;
-sinx; ,cosx=-
,cosx=- .
. ,cosx=-
,cosx=- .
.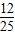 ;
;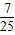 .
.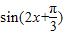 =sin2xcos
=sin2xcos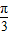 +cos2xsin
+cos2xsin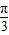
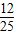 ×
× +(-
+(-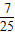 )×
)×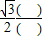
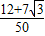 .
.

科目:高中数学 来源: 题型:
| ||
| 4 |
15
| ||
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() .
.
(I)当![]() 时,求函数
时,求函数![]() 的极值;w.w.w.k.s.5.u.c.o.m
的极值;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(II) 若函数![]() 的图象上任意不同的两点连线的斜率都小于2,求证:
的图象上任意不同的两点连线的斜率都小于2,求证:![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() ,且
,且![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
![]()
(1) 试用含![]() 的代数式表示b,并求
的代数式表示b,并求![]() 的单调区间;
的单调区间;
(2)令![]() ,设函数
,设函数![]() 在
在![]() 处取得极值,记点M (
处取得极值,记点M (![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),P(
),P(![]() ),
), ![]() ,请仔细观察曲线
,请仔细观察曲线![]() 在点P处的切线与线段MP的位置变化趋势,并解释以下问题:
在点P处的切线与线段MP的位置变化趋势,并解释以下问题:
(I)若对任意的m ![]() (
(![]() , x
, x![]() ),线段MP与曲线f(x)均有异于M,P的公共点,试确定t的最小值,并证明你的结论;
),线段MP与曲线f(x)均有异于M,P的公共点,试确定t的最小值,并证明你的结论;
(II)若存在点Q(n ,f(n)), x ![]() n< m,使得线段PQ与曲线f(x)有异于P、Q的公共点,请直接写出m的取值范围(不必给出求解过程)w.w.w.k.s.5.u.c.o.m
n< m,使得线段PQ与曲线f(x)有异于P、Q的公共点,请直接写出m的取值范围(不必给出求解过程)w.w.w.k.s.5.u.c.o.m ![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com