Question

（07年湖南卷理）（12分）

已知双曲线的左、右焦点分别为，，过点的动直线与双曲线相交于两点．

（I）若动点满足（其中为坐标原点），求点的轨迹方程；

（II）在轴上是否存在定点，使?为常数？若存在，求出点的坐标；

若不存在，请说明理由．

Answer 1

解析：由条件知，，设，．

解法一：（I）设，则则，，

，由得

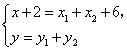即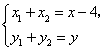

于是的中点坐标为．

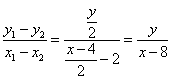当不与轴垂直时，，即．

又因为两点在双曲线上，所以，，两式相减得

，即．

将代入上式，化简得．

当与轴垂直时，，求得，也满足上述方程．

所以点的轨迹方程是．

（II）假设在轴上存在定点，使为常数．

当不与轴垂直时，设直线的方程是．

代入有．

则是上述方程的两个实根，所以，，

于是

．

因为是与无关的常数，所以，即，此时=．

当与轴垂直时，点的坐标可分别设为，，

此时．

故在轴上存在定点，使为常数．

解法二：（I）同解法一的（I）有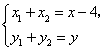

当不与轴垂直时，设直线的方程是．

代入有．

则是上述方程的两个实根，所以．

．

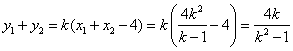由①②③得．…………………………………………………④

．……………………………………………………………………⑤

当时，，由④⑤得，，将其代入⑤有

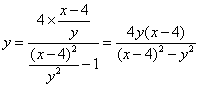．整理得．

当时，点的坐标为，满足上述方程．

当与轴垂直时，，求得，也满足上述方程．

故点的轨迹方程是．

（II）假设在轴上存在定点点，使为常数，

当不与轴垂直时，由（I）有，．

以上同解法一的（II）．