


科目:高中数学 来源: 题型:
| 1 |
| 7 |
5
| ||
| 14 |
| π |
| 2 |
| β |
| 2 |
| 1 |
| 9 |
| α |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4 |
| 3 |
| A、①③ | B、①② | C、③④ | D、①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:
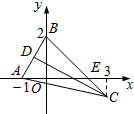 如图所示,已知△ABC中,点D是边AB的中点,边BC与x轴交于点E,∠BEA=45°.求:
如图所示,已知△ABC中,点D是边AB的中点,边BC与x轴交于点E,∠BEA=45°.求:查看答案和解析>>
科目:高中数学 来源: 题型:
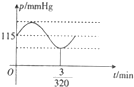 心脏跳动时,血压在增加或减小,血压的最大值和最嚣张分别成为收缩压和舒张压,当读数为120/80mmHg为标准值(收缩压为120mmHg舒张压为80mmHg)设某人的血压满足函数关系式p(t)=a+bsinωt(其中p(t)为血压(mmHg),t为事件(mim)a,b,ω为正常数),其函数图象如图所示,点(
心脏跳动时,血压在增加或减小,血压的最大值和最嚣张分别成为收缩压和舒张压,当读数为120/80mmHg为标准值(收缩压为120mmHg舒张压为80mmHg)设某人的血压满足函数关系式p(t)=a+bsinωt(其中p(t)为血压(mmHg),t为事件(mim)a,b,ω为正常数),其函数图象如图所示,点(| 1 |
| 960 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com