
【题目】若△ABC的三内角A、B、C对应边a、b、c满足2a=b+c,则角A的取值范围为 .
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,已知平面AA1C1C⊥平面ABCD,且 ![]() ,AD=CD=1.
,AD=CD=1.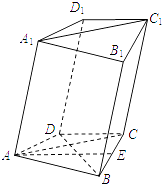
(1)求证:BD⊥AA1;
(2)若E为棱BC的中点,求证:AE∥平面DCC1D1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,且D,E分别是棱A1B1 , A1A1的中点,点F在棱AB上,且AF= ![]() AB.
AB.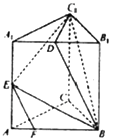
(1)求证:EF∥平面BDC1;
(2)求三棱锥D﹣BEC1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0),过点C(﹣4,0)作抛物线的两条切线CA,CB,A,B为切点,若直线AB经过抛物线y2=2px的焦点,△CAB的面积为24,则以直线AB为准线的抛物线标准方程是( )
A.y2=4x
B.y2=﹣4x
C.y2=8x
D.y2=﹣8x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcosθ=a(a>0),Q为l上一点,以OQ为边作等边三角形OPQ,且O、P、Q三点按逆时针方向排列.
(Ⅰ)当点Q在l上运动时,求点P运动轨迹的直角坐标方程;
(Ⅱ)若曲线C:x2+y2=a2 , 经过伸缩变换 ![]() 得到曲线C′,试判断点P的轨迹与曲线C′是否有交点,如果有,请求出交点的直角坐标,没有则说明理由.
得到曲线C′,试判断点P的轨迹与曲线C′是否有交点,如果有,请求出交点的直角坐标,没有则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知点P(1,﹣2),直线l: ![]() (m 为参数),以坐标原点为极点,以 x轴的正半轴为极轴建立极坐标系;曲线C的极坐标方程为ρsin2θ=3cosθ;直线l与曲线C的交点为A,B.
(m 为参数),以坐标原点为极点,以 x轴的正半轴为极轴建立极坐标系;曲线C的极坐标方程为ρsin2θ=3cosθ;直线l与曲线C的交点为A,B.
(1)求直线l和曲线C的普通方程;
(2)求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知曲线 ![]() (α为参数),在以O为极点,x轴正半轴为极轴的极坐标系中,曲线
(α为参数),在以O为极点,x轴正半轴为极轴的极坐标系中,曲线 ![]() ,曲线C3:ρ=2sinθ.
,曲线C3:ρ=2sinθ.
(1)求曲线C1与C2的交点M的直角坐标;
(2)设点A,B分别为曲线C2 , C3上的动点,求|AB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD, ![]() ,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF=1.
,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF=1.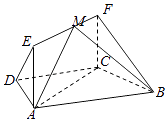
(1)求证:EF⊥平面BCF;
(2)点M在线段EF(含端点)上运动,当点M在什么位置时,平面MAB与平面FCB所成锐二面角最大,并求此时二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com