练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如下图，椭圆＝1(a＞b＞0)与过点A(2，0)，B(0，1)的直线有且只有一个公共点T，且椭圆的离心率e＝，

    (1)求椭圆的方程；

    (2)设F1、F2分别为椭圆的左、右焦点，求证：|AT|2＝|AF1||AF2|．

    答案：
    解析：

    　　(1)解析：过A、B的直线方程为＋y＝1，

    　　因为由题意得有唯一解，

    　　即(b2＋a2)x2－a2x＋a2－a2b2＝0有唯一解，

    　　所以Δ＝a2b2(a2＋4b2－4)＝0(ab≠0)．

    　　故a2＋4b2－4＝0．

    　　又因为c＝，即＝，

    　　所以a2＝4b2．从而得a2＝2，b2＝，故所求的椭圆方程为＝1．

    　　(2)证明：由(1)得c＝，所以F1(－，0)，F2(，0)，

    　　由解得x1＝x2＝1，

    　　因此T(1，)．

    　　从而|AT|2＝，

    　　因为|AF1|·|AF2|＝，

    　　所以|AT|2＝|AF1|·|AF2|．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：学习周报　数学　北师大课标高二版(选修1－2)　2009－2010学年　第31期　总第187期 北师大课标 题型：013

    椭圆＝1(a＞b＞0)的面积S＝πab，当a＝4，b＝2时，计算椭圆面积的流程图如下图，则括号内应填入

    [　　]
    A．

    B．

    C．

    D．

    查看答案和解析>>

    科目：高中数学 来源：导学大课堂选修数学1-1苏教版 苏教版 题型：044

    学校科技小组在计算机上模拟航天器变轨返回试验．设计方案如下图：航天器运动(按顺时针方向)的轨迹方程为＝1，变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、M(0，)为顶点的抛物线的实线部分，降落点为D(8，0)．观测点A(4，0)、B(6，0)同时跟踪航天器．

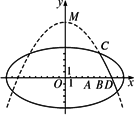
    (1)求航天器变轨后的运行轨迹所在的曲线方程；

    (2)试问：当航天器在x轴上方时，观测点A、B测得离航天器的距离分别为多少时，应向航天器发出变轨指令？

    查看答案和解析>>

    科目：高中数学 来源：全优设计选修数学－2-1苏教版 苏教版 题型：044

    如下图，点A、B分别是椭圆＝1长轴的左、右端点，点F是椭圆的右焦点，点P在椭圆上，且位于x轴上方，PA⊥PF．

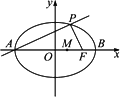
    (1)求点P的坐标；

    (2)设M是椭圆长轴AB上的一点，M到直线AP的距离等于|MB|，求椭圆上的点到点M的距离d的最小值．

    查看答案和解析>>

    科目：高中数学 来源：全优设计选修数学－2-1苏教版 苏教版 题型：044

    2003年10月15日9时，“神舟”五号载人飞船发射升空，于9时9分50秒准确进入预定轨道，开始巡天飞行，该轨道是以地球的中心F2为一个焦点的椭圆．选取坐标系如下图，椭圆中心在原点，近地点A距地面200 km，远地点B距地面350 km．已知地球半径R＝6371 km．

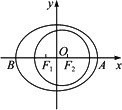
    (1)求飞船飞行的椭圆轨道的方程；

    (2)飞船绕地球飞行了十四圈后，于16日5时59分返回舱与推进舱分离，结束巡天飞行，飞船共巡天飞行了约6×105 km，问飞船巡天飞行平均速度是多少？(结果精确到1 km/s)

    查看答案和解析>>

    同步练习册答案