
【题目】已知圆![]() 过
过![]() 两点,且圆心
两点,且圆心![]() 在直线
在直线![]() 上
上
(1)求圆![]() 的方程
的方程
(2)若直线![]() 过点
过点![]() 且被圆
且被圆![]() 截得的线段长为
截得的线段长为![]() ,求
,求![]() 的方程
的方程

【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)把点![]() 、
、![]() 的坐标代入圆的标准方程,圆心坐标代入直线
的坐标代入圆的标准方程,圆心坐标代入直线![]() ,利用待定系数法求得系数的值;
,利用待定系数法求得系数的值;
(2)分类讨论,斜率存在和斜率不存在两种情况.
①当直线![]() 的斜率不存在时,满足题意,易得直线方程;
的斜率不存在时,满足题意,易得直线方程;
②当直线![]() 的斜率存在时,设所求直线
的斜率存在时,设所求直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为:
的方程为:![]() ,由点到直线的距离公式求得
,由点到直线的距离公式求得![]() 的值.
的值.
(1)设圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为
,半径为![]()
设圆![]() 的方程为
的方程为![]()
由题意可得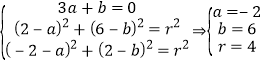
所以圆![]() 方程为
方程为![]() .
.
(2)因为直线![]() 经过点
经过点![]() ,且被圆
,且被圆![]() 截得的线段长为
截得的线段长为![]()
![]() 圆心
圆心![]() 到直线的距离为
到直线的距离为![]()
当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 的方程为
的方程为![]() (8分)
(8分)
此时圆心到直线的距离恰好为2,符合条件
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]()
则圆心![]() 到直线
到直线![]() 的距离为
的距离为![]()
即![]() 此时直线
此时直线![]() 的方程为
的方程为![]() (11分)
(11分)
综上所述直线![]() 的方程为
的方程为![]() 或
或![]()


科目:高中数学 来源: 题型:
【题目】如图,直线AB经过⊙O上一点C,⊙O的半径为3,△AOB是等腰三角形,且C是AB中点,⊙O交直线OB于E、D. 
(1)证明:直线AB与⊙O相切;
(2)若∠CED的正切值为 ![]() ,求OA的长.
,求OA的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,AB=1,BC=2,∠CBA= ![]() ,ABEF为直角梯形,BE∥AF,∠BAF=
,ABEF为直角梯形,BE∥AF,∠BAF= ![]() ,BE=2,AF=3,平面ABCD⊥平面ABEF.
,BE=2,AF=3,平面ABCD⊥平面ABEF. 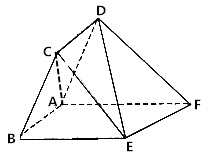
(1)求证:AC⊥平面ABEF;
(2)求平面ABCD与平面DEF所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代名词“刍童”原来是草堆的意思,关于“刍童”体积计算的描述,《九章算术》注曰:“倍上袤,下袤从之,亦倍下袤,上袤从之,各以其广乘之,并,以高乘之,皆六而一.”其计算方法是:将上底面的长乘二,与下底面的长相加,再与上底面的宽相乘,将下底面的长乘二,与上底面的长相加,再与下底面的宽相乘;把这两个数值相加,与高相乘,再取其六分之一.已知一个“刍童”的下底面是周长为18的矩形,上底面矩形的长为3,宽为2,“刍童”的高为3,则该“刍童”的体积的最大值为
A. ![]() B.
B. ![]() C. 39 D.
C. 39 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学四年级男同学有45名,女同学有30名,老师按照分层抽样的方法组建了一个5人的课外兴趣小组.
(Ⅰ)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(Ⅱ)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出1名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
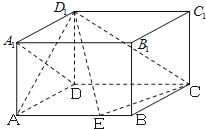
【题目】已知在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(Ⅰ)求证:D1E⊥A1D;
(Ⅱ)在棱AB上是否存在点E使得AD1与平面D1EC成的角为![]() ?若存在,求出AE的长,若不存在,说明理由.
?若存在,求出AE的长,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家![]() 和3个欧洲国家
和3个欧洲国家![]() 中选择2个国家去旅游.
中选择2个国家去旅游.
(Ⅰ)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(Ⅱ)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括![]() 但不包括
但不包括![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com