
一个袋中装有10个大小相同的小球.其中白球5个、黑球4个、红球1个.
(1)从袋中任意摸出2个球,求至少得到1个白球的概率;
(2)从袋中任意摸出3个球,记得到白球的个数为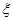 ,求随机变量
,求随机变量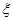 的数学期望
的数学期望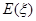 .
.
 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:解答题
湖南省在学业水平考查中设计了物理学科的实验考查方案:考生从 道备选试验考查题中一次随机抽取
道备选试验考查题中一次随机抽取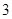 题,并按照题目要求独立完成全部实验操作.规定:至少正确完成其中
题,并按照题目要求独立完成全部实验操作.规定:至少正确完成其中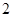 题便通过考查.已知
题便通过考查.已知 道备选题中文科考生甲有
道备选题中文科考生甲有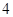 题能正确完成,
题能正确完成,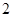 题不能完成;文科考生乙每题正确完成的概率都是
题不能完成;文科考生乙每题正确完成的概率都是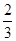 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(Ⅰ)分别写出文科考生甲正确完成题数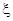 和文科考生乙正确完成题数
和文科考生乙正确完成题数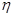 的概率分布列,并计算各自的数学期望;
的概率分布列,并计算各自的数学期望;
(Ⅱ)试从两位文科考生正确完成题数的数学期望及通过考查的概率分析比较这两位考生的实验操作能力.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
气象部门提供了某地今年六月份(30天)的日最高气温的统计表如下:
| 日最高气温t (单位:℃) | t 22℃ 22℃ | 22℃<t 28℃ 28℃ | 28℃<t 32℃ 32℃ | 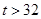 ℃ ℃ |
| 天数 | 6 | 12 | 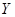 | 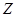 |
| 日最高气温t (单位:℃) | t 22℃ 22℃ | 22℃<t 28℃ 28℃ | 28℃<t 32℃ 32℃ | 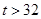 ℃ ℃ |
日销售额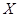 (千元) (千元) | 2 | 5 | 6 | 8 |
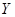 ,
, 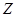 的值;
的值;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设有关于x的一元二次方程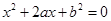 .
.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知A,B,C,D四个城市,它们各自有一个著名的旅游点,依次记为A,b,C,D,把A,B,C,D和A,b,C,D分别写成左、右两列.现在一名旅游爱好者随机用4条线把城市与旅游点全部连接起来, 构成“一一对应”.规定某城市与自身的旅游点相连称为“连对”,否则称为“连错”,连对一条得2分,连错一条得0分.
(Ⅰ)求该旅游爱好者得2分的概率.
(Ⅱ)求所得分数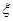 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现有甲、乙两个靶.某射手向甲靶射击两次,每次命中的概率为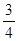 ,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为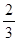 ,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(I)求该射手恰好命中两次的概率;
(II)求该射手的总得分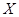 的分布列及数学期望
的分布列及数学期望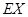 ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一次数学考试中,第22,23,24题为选做题,规定每位考生必须且只须在其中选做一题,设5名考生选做这三题的任意一题的可能性均为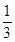 ,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.
,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.
(1)求其中甲、乙两人选做同一题的概率;
(2)设选做第23题的人数为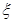 ,求
,求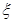 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有一条的为第一层,有二条的为第二层, ,依次类推.现有一颗小弹子从第一层的通道里向下运动,若在通道的分叉处,小弹子以相同的概率落入每个通道.记小弹子落入第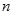 层第
层第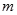 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为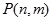 ,某研究性学习小组经探究发现小弹子落入第
,某研究性学习小组经探究发现小弹子落入第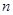 层的第
层的第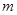 个通道的次数服从二项分布,请你解决下列问题.
个通道的次数服从二项分布,请你解决下列问题.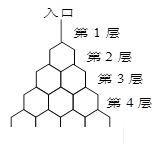
(Ⅰ)试求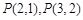 及
及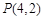 的值,并猜想
的值,并猜想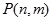 的表达式;(不必证明)
的表达式;(不必证明)
(Ⅱ)设小弹子落入第6层第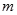 个竖直通道得到分数为
个竖直通道得到分数为 ,其中
,其中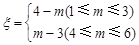 ,试求
,试求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com