
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有一条的为第一层,有二条的为第二层, ,依次类推.现有一颗小弹子从第一层的通道里向下运动,若在通道的分叉处,小弹子以相同的概率落入每个通道.记小弹子落入第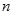 层第
层第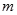 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为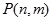 ,某研究性学习小组经探究发现小弹子落入第
,某研究性学习小组经探究发现小弹子落入第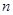 层的第
层的第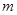 个通道的次数服从二项分布,请你解决下列问题.
个通道的次数服从二项分布,请你解决下列问题.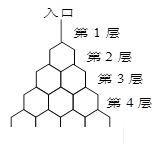
(Ⅰ)试求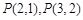 及
及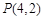 的值,并猜想
的值,并猜想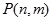 的表达式;(不必证明)
的表达式;(不必证明)
(Ⅱ)设小弹子落入第6层第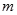 个竖直通道得到分数为
个竖直通道得到分数为 ,其中
,其中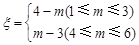 ,试求
,试求 的分布列及数学期望.
的分布列及数学期望.
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
一个袋中装有10个大小相同的小球.其中白球5个、黑球4个、红球1个.
(1)从袋中任意摸出2个球,求至少得到1个白球的概率;
(2)从袋中任意摸出3个球,记得到白球的个数为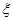 ,求随机变量
,求随机变量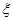 的数学期望
的数学期望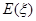 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知某校在一次考试中,5名学生的数学和物理成绩如下表:
| 学生的编号i | 1 | 2 | 3 | 4 | 5 |
| 数学成绩x | 80 | 75 | 70 | 65 | 60 |
| 物理成绩y | 70 | 66 | 68 | 64 | 62 |
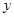 关于
关于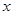 的线性回归方程
的线性回归方程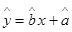 ,
,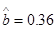
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
今年我国部分省市出现了人感染H7N9禽流感确诊病例,各地家禽市场受其影响生意冷清.A市虽未发现H7N9疑似病例,但经抽样有20%的市民表示还会购买本地家禽.现将频率视为概率,解决下列问题:
(Ⅰ)从该市市民中随机抽取3位,求至少有一位市民还会购买本地家禽的概率;
(Ⅱ)从该市市民中随机抽取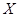 位,若连续抽取到两位愿意购买本地家禽的市民,或抽取的人数达到4位,则停止抽取,求
位,若连续抽取到两位愿意购买本地家禽的市民,或抽取的人数达到4位,则停止抽取,求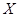 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校高三学生体检后,为了解高三学生的视力情况,该校从高三六个班的300名学生中以班为单位(每班学生50人),每班按随机抽样抽取了8名学生的视力数据.其中高三(1)班抽取的8名学生的视力数据与人数见下表:
| 视力数据 | 4.0 | 4.1 | 4.2 | 4.3 | 4.4 | 4.5 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 | 5.1 | 5.2 | 5.3 |
| 人数 | | | | | 2 | | 2 | | 2 | 1 | | 1 | | |
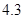 、
、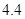 、
、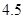 、
、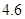 、
、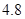 .若从这六个班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于
.若从这六个班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于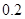 的概率.
的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人进行围棋比赛,规定每局胜者得1分,负者得0分,比赛进行到有一方比对方多2分或打满6局时停止.设甲在每局中获胜的概率为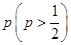 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为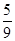 .
.
(Ⅰ)求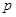 的值;
的值;
(Ⅱ)设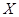 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量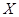 的分布列和数学期望
的分布列和数学期望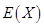 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生
(I)分别求出按程序框图正确编程运行时输出y的值为i的概率pi(i=1,2,3);
(II)甲乙两同学依据自己对程序框图的理解,各自编程写出程序重复运行n次后,统计记录输出y的值为i(i=1,2,3)的频数,以下是甲乙所作频数统计表的部分数据.
甲的频数统计图(部分)
| 运行次数n | 输出y的值为1的频数 | 输出y的值为2的频数 | 输出y的值为3的频数 |
| 30 | 14 | 6 | 10 |
| … | … | … | … |
| 2100 | 1027 | 376 | 697 |
| 运行次数n | 输出y的值为1的频数 | 输出y的值为2的频数 | 输出y的值为3的频数 |
| 30 | 12 | 11 | 7 |
| … | … | … | … |
| 2100 | 1051 | 696 | 353 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某研究性学习小组对昼夜温差与某种子发芽数的关系进行研究,他们分别记录了四天中每天昼夜温差与每天100粒种子浸泡后的发芽数,得到如下资料:
| 时间 | 第一天 | 第二天 | 第三天 | 第四天 |
| 温差(℃) | 9 | 10 | 8 | 11 |
| 发芽数(粒) | 33 | 39 | 26 | 46 |
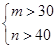 ”的事件A的概率.
”的事件A的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某集团公司举办一次募捐爱心演出,有1000人参加,每人一张门票,每张100元。在演出过程中穿插抽奖活动,第一轮抽奖从这1000张票根中随机抽取10张,其持有者获得价值1000元的奖品,并参加第二轮抽奖活动。第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个数 (
(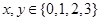 ),满足
),满足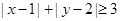 电脑显示“中奖”,且抽奖者获得特等奖奖金;否则电脑显示“谢谢”,则不中奖。
电脑显示“中奖”,且抽奖者获得特等奖奖金;否则电脑显示“谢谢”,则不中奖。
(1)已知小明在第一轮抽奖中被抽中,求小明在第二轮抽奖中获奖的概率;
(2)若该集团公司望在此次活动中至少获得61875元的收益,则特等奖奖金最高可设置成多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com