
某集团公司举办一次募捐爱心演出,有1000人参加,每人一张门票,每张100元。在演出过程中穿插抽奖活动,第一轮抽奖从这1000张票根中随机抽取10张,其持有者获得价值1000元的奖品,并参加第二轮抽奖活动。第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个数 (
(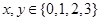 ),满足
),满足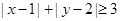 电脑显示“中奖”,且抽奖者获得特等奖奖金;否则电脑显示“谢谢”,则不中奖。
电脑显示“中奖”,且抽奖者获得特等奖奖金;否则电脑显示“谢谢”,则不中奖。
(1)已知小明在第一轮抽奖中被抽中,求小明在第二轮抽奖中获奖的概率;
(2)若该集团公司望在此次活动中至少获得61875元的收益,则特等奖奖金最高可设置成多少元?
(1)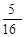 (2)a≤9900
(2)a≤9900
解析试题分析:(Ⅰ)从0,1,2,3四个数字中有重复取2个数字,其基本事件有(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3),(2,0),(2,1),(2,2),(2,3),(3,0),(3,1),(3,2),(3,3)共 16 个.
设“小明在第二轮抽奖中获奖”为事件A,且事件A所包含的基本事件有(0,0),(2,0),(3,0),(3,1),(3,3)共5个,∴P(A)=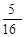 .
.
(Ⅱ)设特等奖奖金为a元,一个人参加此次活动的收益为ξ,则ξ的可能取值为-100,900,a.
P(ξ=-100)= ,P(ξ=900)=
,P(ξ=900)=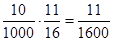 ,P(ξ="a)="
,P(ξ="a)=" 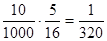 .
.
∴ξ的分布列为
∴ξ -100 900 a P 
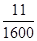
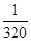
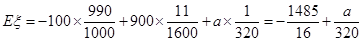 .
.
∴该集团公司收益的期望为 ,
,
由题意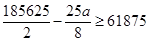 ,解得a≤9900.
,解得a≤9900.
故特等奖奖金最高可设置成9900元.
考点:古典概型和分布列
点评:主要是考查了古典概型概率和分布列的运用,属于中档题。


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:解答题
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有一条的为第一层,有二条的为第二层, ,依次类推.现有一颗小弹子从第一层的通道里向下运动,若在通道的分叉处,小弹子以相同的概率落入每个通道.记小弹子落入第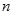 层第
层第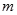 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为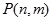 ,某研究性学习小组经探究发现小弹子落入第
,某研究性学习小组经探究发现小弹子落入第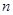 层的第
层的第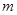 个通道的次数服从二项分布,请你解决下列问题.
个通道的次数服从二项分布,请你解决下列问题.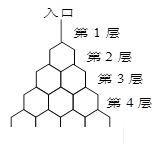
(Ⅰ)试求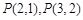 及
及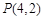 的值,并猜想
的值,并猜想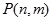 的表达式;(不必证明)
的表达式;(不必证明)
(Ⅱ)设小弹子落入第6层第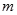 个竖直通道得到分数为
个竖直通道得到分数为 ,其中
,其中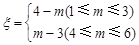 ,试求
,试求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
每一个父母都希望自己的孩子能升上比较理想的中学,于是就催生了“择校热”,这样“择校”的结果就导致了学生在路上耽误的时间增加了.若某生由于种种原因,每天只能6:15骑车从家出发到学校,途经5个路口,这5个路口将家到学校分成了6个路段,每个路段的骑车时间是10分钟(通过路口的时间忽略不计),假定他在每个路口遇见红灯的概率均为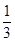 ,且该生只在遇到红灯或到达学校才停车.对每个路口遇见红灯的情况统计如下:
,且该生只在遇到红灯或到达学校才停车.对每个路口遇见红灯的情况统计如下:
| 红灯 | 1 | 2 | 3 | 4 | 5 |
| 等待时间(秒) | 60 | 60 | 90 | 30 | 90 |
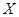 表示该学生第一次停车时已经通过的路口数,求它的分布列与期望.
表示该学生第一次停车时已经通过的路口数,求它的分布列与期望.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某小组共有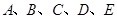 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
如下表所示:
| | A | B | C | D | E |
| 身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
| 体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
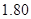 的同学中任选
的同学中任选 人,求选到的
人,求选到的 人身高都在
人身高都在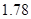 以下的概率
以下的概率 人,求选到的
人,求选到的 人的身高都在
人的身高都在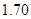 以上且体重指标都在
以上且体重指标都在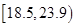 中的概率.
中的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高校数学系计划在周六和周日各举行一次主题不同的心理测试活动,分别由李老师和张老师负责,已知该系共有 位学生,每次活动均需该系
位学生,每次活动均需该系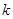 位学生参加(
位学生参加( 和
和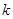 都是固定的正整数).假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系
都是固定的正整数).假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系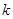 位学生,且所发信息都能收到.记该系收到李老师或张老师所发活动通知信息的学生人数为
位学生,且所发信息都能收到.记该系收到李老师或张老师所发活动通知信息的学生人数为
(Ⅰ)求该系学生甲收到李老师或张老师所发活动通知信息的概率;
(Ⅱ)求使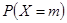 取得最大值的整数
取得最大值的整数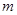 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一次购物抽奖活动中,假设某6张券中有一等奖 券1张,可获价值50元的奖品;有二等奖券1张,每张可获价值20元的奖品;其余4张没有奖.某顾客从此6张中任抽1张,求:
(1)该顾客中奖的概率;
(2)该顾客参加此活动可能获得的奖品价值的期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人各进行3次射击,甲每次击中目标的概率为 ,乙每次击中目标的概率为
,乙每次击中目标的概率为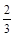
求:(1)乙至少击中目标2次的概率;
(2)乙恰好比甲多击中目标2次的概率
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂有甲、乙两个生产小组,每个小组各有四名工人,某天该厂每位工人的生产情况如下表.
| | 员工号 | 1 | 2 | 3 | 4 |
| 甲组 | 件数 | 9 | 11 | 1l | 9 |
| | 员工号 | 1 | 2 | 3 | 4 |
| 乙组 | 件数 | 9 | 8 | 10 | 9 |
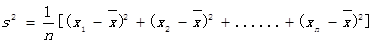 ,其中
,其中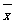 为x1,x2, ,xn的平均数)
为x1,x2, ,xn的平均数)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球. 规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得-1分 . 现从盒内任取3个球
(Ⅰ)求取出的3个球中至少有一个红球的概率;
(Ⅱ)求取出的3个球得分之和恰为1分的概率;
(Ⅲ)设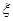 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求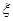 的分布列.
的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com