
如图,在△ 中,
中, 是
是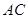 的中点,
的中点,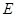 是
是 的中点,
的中点, 的延长线交
的延长线交 于
于 .
.

(Ⅰ)求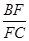 的值;(4分)
的值;(4分)
(Ⅱ)若△ 的面积为
的面积为 ,
四边形
,
四边形 的面积为
的面积为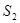 ,求
,求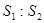 的值.
(6分)
的值.
(6分)
证明:(Ⅰ)过D点作DG∥BC,并交AF于G点,
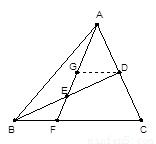
∵E是BD的中点,∴BE=DE,
又∵∠EBF=∠EDG,∠BEF=∠DEG,
∴△BEF≌△DEG,则BF=DG, ∴BF: FC=DG:FC, 又∵D是AC的中点,则DG:FC=1:2, 则BF:FC=1:2;即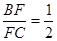 (4分)
(4分)
(Ⅱ)若△BEF以BF为底,△BDC以BC为底,则由(1)知BF:BC=1:3,又由BE:BD=1:2可知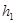 :
: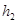 =1:2,其中
=1:2,其中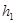 、
、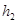 分别为△BEF和△BDC的高,则
分别为△BEF和△BDC的高,则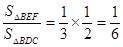 ,则
,则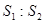 =1:5.(10分)
=1:5.(10分)
【解析】(I)过D作GD//BF,并交AF于G点,则易知BF=GD,所以本题转化为求DG:FC的值.
(II)本题可转化为求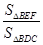 ,然后△BEF以BF为底,△BDC以BC为底,则由(1)知BF:BC=1:3,又由BE:BD=1:2可知
,然后△BEF以BF为底,△BDC以BC为底,则由(1)知BF:BC=1:3,又由BE:BD=1:2可知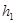 :
: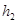 =1:2,问题到此基本得以解决
=1:2,问题到此基本得以解决


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源:2010年吉林省东北师大附中高一下学期期中考试数学 题型:解答题
(本题满分8分)
如图,在正方体 中,
中,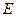 是
是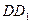 的中点,
的中点,
求证: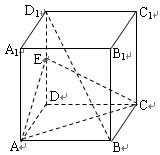
(1)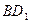 ∥平面
∥平面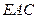 ;
;
(2)求异面直线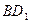 与
与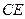 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2013届福建省高二上学期期末考试理科数学 题型:解答题
.(本小题满分13分)如图,在正方体 中,
中, 是
是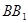 的中点。
的中点。
(Ⅰ)在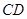 上求一点
上求一点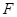 ,使
,使 平面
平面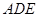 ;
;
(Ⅱ)求二面角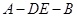 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源:辽宁省抚顺市六校联合体2009-2010学年度高三二模(数学理)试题 题型:解答题
(12分)如图,在梯形 中,
中, 是
是 的中点,将
的中点,将 沿
沿 折起,使点
折起,使点 到点
到点 的位置,使二面角
的位置,使二面角 的大小为
的大小为
(1)求证: ;
;
(2)求直线 与平面
与平面 所成角的正弦值
所成角的正弦值

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com