练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    对于给定的自然数，如果数列满足：的任意一个排列都可以在原数列中删去若干项后按数列原来顺序排列而得到，则称是“的覆盖数列”。如1,2,1 是“2的覆盖数列”；1,2,2则不是“2的覆盖数列”，因为删去任何数都无法得到排列2,1，则以下四组数列中是 “3的覆盖数列” 为（   ）
    A．1,2,3,3,1,2,3B．1,2,3,2,1,3,1
    C．1,2,3,1,2,1,3D．1,2,3,2,2,1,3
    C

    解：由定义得，A不是“3的覆盖数列”，因为删去任何数都无法得到排列3，2，1．
    B不是“3的覆盖数列”，因为删去任何数都无法得到排列3，1，2；
    D不是“3的覆盖数列”，因为删去任何数都无法得到排列3，1，2；
    而C则符合要求．
    故选 C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：单选题

    设，，，……，，
    (n∈N)，则f2012(x) =（   ）.
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知数列是等差数列, ，从中依次取出第3项，第9项，第27项，……第项按原来的顺序排成一个新数列，则（   ）
    A．　B．　 　C．+2D．-2

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    若1，a，3成等差数列；1，b，4成等比数列，则的值（    ）  
    A．B．C．1D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设a1，a2，…，a50是从－1，0，1这三个整数中取值的数列，若a1+a2+…+a50=9，
    且（a1+1）2+（a2+1）2+…+（a50+1）2=107，则a1，a2，…，a50中有0的个数为（   ）   
    A．10B．11 C．12D．13

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知线段AB上有10个确定的点（包括端点A与B）. 现对这些点进行往返标数（从A→B→A→B→…进行标数，遇到同方向点不够数时就“调头”往回数）。如图：在点A上标1，称为点1，然后从点1开始数到第二个数，标上2，称为点2，再从点2开始数到第三个数，标上3，称为点3（标上数n的点称为点n），……，这样一直继续下去，直到1，2，3，…，2012都被标记到点上．则点2012上的所有标记的数中，最小的是    ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知数列{an}的前n项和为Sn，且Sn＝2an－2，则an＝         ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

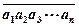    记为一个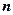位正整数，其中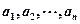都是正整数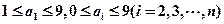，．若对任意的正整数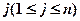，至少存在另一个正整数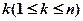，使得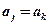，则称这个数为“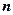位重复数”．根据上述定义，“四位重复数”的个数为             （    ）
    A．1994个B．4464个C．4536个D．9000个

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    在数列{}中，=2，+1=+Ln(1+)，则=
    A．2+LnnB．2+(n－1LnnC．2+nLnnD．1+n+Lnn

    查看答案和解析>>

    同步练习册答案