Question

设函数f(x)=asin(kx+)，g(x)=btan(kx-)（k＞0），它们的最小正周期分别为T₁、T₂，且T₁+T₂=，已知f()=g(),f()=.

（1）求f(x),g(x)的解析式；

（2）f(x)的图象可由函数y=sinx(x∈R)的图象经过怎样的平移伸缩变换得到？

Answer 1

思路分析：考查三角函数的性质及三角函数图象的变换，可根据题目的条件确定a、b、k的值.

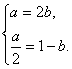解：（1）由已知可得，则k=2，且有整理得解得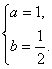

所以f(x)=sin(2x+)，g(x)=tan(2x-).

（2）方法一：将函数y=sinx(x∈R)的图象向左平移个单位，得到函数y=sin(x+)的图象，再将函数y=sin(x+)图象上所有点的横坐标变为原来的（纵坐标不变）,即可得函数f(x)=sin(2x+)的图象.

方法二：将函数y=sinx(x∈R)图象上所有点的横坐标变为原来的（纵坐标不变）,得到函数y=sin2x的图象，再将函数y=sin2x的图象向左平移个单位即可得函数f(x)=sin(2x+)的图象.

方法归纳 求三角函数的周期，通常把它转化成一个角的一个函数的形式，周期的大小仅与x的系数有关；求未知数的值，列含有该未知数的等式，这就是方程的思想.

平移变换只是变换自变量x或函数y，与它们的系数无关.