练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    四边形ABCD中，对角线AC、BD相交于点O，给出下列四个条件：①AD∥BC；②AD=BC；③OA=OC；④OB=OD．从中任选两个条件，能使四边形ABCD为平行四边形的选法有（　　）
    A、3种B、4种C、5种D、6种
    分析：根据题目所给条件，利用平行四边形的判定方法分别进行分析即可．
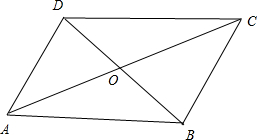    解答：精英家教网解：：①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形．
    ③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形．
    ①③可证明△ADO≌△CBO，进而得到AD=CB，可利用一组对边平行且相等的四边形是平行四边形，
    判定出四边形ABCD为平行四边形．
    ①④可证明△ADO≌△CBO，进而得到AD=CB，可利用一组对边平行且相等的四边形是平行四边形，
    判定出四边形ABCD为平行四边形．
    故选：B．
    点评：此题主要考查了平行四边形的判定，关键是熟练掌握平行四边形的判定定理，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    9、如图，平行四边形ABCD中，AB⊥BD，沿BD将△ABD折起，使面ABD⊥面BCD，连接AC，则在四面体ABCD的四个面中，互相垂直的平面有（　　）对．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    圆内接四边形ABCD中，BA与CD的延长线交于点P，AC与BD交于点E，则图中相似三角形有（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题中，错误的命题是
    ④
    ④
    ．
    ①在四边形ABCD中，若
    AC
    =
    AB
    +
    AD
    ，则ABCD为平行四边形
    ②已知
    a
    ，
    b
    ，
    a
    +
    b
    为非零向量，且a+b平分a与b的夹角，则|a|=|b|
    ③已知a与b不共线，则a+b与a-b不共线
    ④对实数λ1，λ2，λ3，则三向量λ1λ2，λ2b-λ3c，λ3c-λ1a不一定在同一平面上．

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

    在空间四边形ABCD中, 若对边AC⊥BD, AB⊥CD, 则对角线AD与BC所成的角是

    [　　]

    A.30°　　B.45°　　C.60°　　D.90°

    查看答案和解析>>

    科目：高中数学 来源：新课程高中数学疑难全解 题型：022

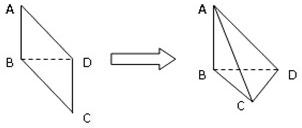
    如图，空间四边形ABCD中，下列条件下EFGH构成的图形是什么？

    (1)点E、F、G、H分别为边AB、BC、CD、DA的中点．

    ①四边形EFGH为________；

    ②四边形EFGH中，四边的平方和等于对角线的平方和．

    ③如果AC＝BD，那么四边形EFGH为________；

    ④如果AC⊥BD，那么四边形EFGH为________；

    ⑤如果AC＝BD，AC⊥BD，那么四边形EFGH为________；

    ⑥如果AB＝BC＝CD＝DA＝AC＝BD，那么四边形EFGH为________；

    ⑦空间四边形ABCD中，对边中点的连线交于一点．

    (2)若E在AB上，H在AD上，F在BC上，G在CD上，且＝＝p，＝＝q．如果p＝q，那么四边形EFGH为________．如果p≠q，那么四边形EFGH为________，并且EF、GH、AC交于一点．

    查看答案和解析>>

    同步练习册答案