
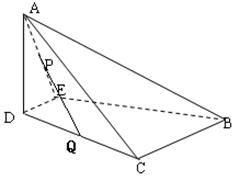
如图,沿等腰直角三角形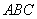 的中位线
的中位线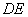 ,将平面
,将平面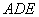 折起,使得平面
折起,使得平面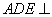 平面
平面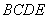 得到四棱锥
得到四棱锥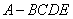 .
.
(1)求证:平面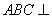 平面
平面 ;
;
(2)过 的中点
的中点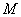 的平面
的平面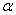 与平面
与平面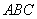 平行,试求平面
平行,试求平面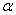 与四棱锥
与四棱锥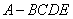 各个面的交线所围成多边形的面积与三角形
各个面的交线所围成多边形的面积与三角形 的面积之比。
的面积之比。
(3)求二面角 的余弦值。
的余弦值。
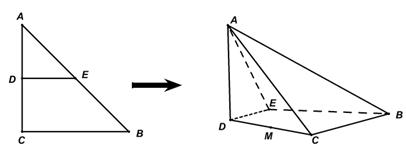
【解析】(1) ,平面
,平面 平面
平面 ,
,
根据两个平面垂直的性质定理得 平面
平面 ,
,
所以 ,又
,又 ,根据线面垂直的判定定理
,根据线面垂直的判定定理 平面
平面 ,
,
 平面
平面 ,所以平面
,所以平面 平面
平面 。
。
(2)由于平面 平面
平面 ,故平面
,故平面 与平面
与平面 的交线
的交线
 ,
,
 是
是 的中点,故
的中点,故 是
是 的中点;同理平面
的中点;同理平面 与平面
与平面 的交线
的交线 ,
,
 为
为 的中点;平面
的中点;平面 的交线
的交线 ,
, 为
为 的中点,
的中点,
连接 即为平面
即为平面 与平面
与平面 的交线,
的交线,
故平面 与四棱锥
与四棱锥 各个面的交线所围成多边形是图中的四边形
各个面的交线所围成多边形是图中的四边形 ,
,
由于 ,故
,故 ,根据(1)
,根据(1) ,
,
由 ,故
,故 ,即四边形
,即四边形 `是直角梯形。
`是直角梯形。
设 ,则
,则 ,
,
 故四边形
故四边形 的面积是
的面积是 ,
,
三角形 的面积是
的面积是 ,
,
故平面 与四棱锥
与四棱锥 各个面
各个面
的交线所围成多边形的面积与
三角形 的面积之比为
的面积之比为 。
。
(3)方法1. 平面
平面 ,
, ,
,
 过点
过点 做
做 的垂线交
的垂线交 的延长线于点
的延长线于点 ,
,
连接 ,则
,则 平面
平面 ,
,
从而 ,
,
所以 即为二面角
即为二面角 的平面角。
的平面角。
设 ,则
,则
 ,则
,则 ,
,
故二面角 的余弦值等于
的余弦值等于 。
。
方法2.建立如图所示的空间直角坐标系,用空间向量法求解。
设 ,则
,则 ,
, ,
, ,
, ,
,
 设
设 为平面
为平面 的法向量,
的法向量,
则 且
且 ,
,
即 且
且 ,
,
取 ,则
,则 ,
,
即平面 的一个法向量为
的一个法向量为 ,(10分)
,(10分)
又 为平面
为平面 的一个法向量,
的一个法向量,
二面角 是锐二面角,故其余弦值为
是锐二面角,故其余弦值为 。
。


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省高三第四次月考理科数学试题(解析版) 题型:解答题
(本小题满分14分)
如图,沿等腰直角三角形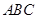 的中位线
的中位线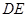 ,将平面
,将平面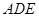 折起,平面
折起,平面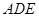 ⊥平面
⊥平面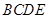 ,得到四棱锥
,得到四棱锥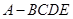 ,
,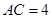 ,设
,设 、
、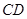 的中点分别为
的中点分别为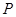 、
、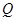 ,
,

(1)求证:平面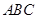 ⊥平面
⊥平面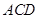
(2)求证:
(3)求平面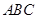 与平面
与平面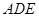 所成锐二面角的余弦值。
所成锐二面角的余弦值。
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高三下学期数学单元测试1-文科 题型:解答题
如图,沿等腰直角三角形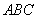 的中位线
的中位线 ,将平面
,将平面 折起,使得平面
折起,使得平面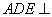 平面
平面 得到四棱锥
得到四棱锥 .
.
(1)求证:平面 平面
平面 ;
;
(2)过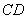 的中点
的中点 的平面
的平面 与平面
与平面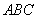 平行,试求平面
平行,试求平面 与四棱锥
与四棱锥 各个面的交线所围成多边形的面积与三角形
各个面的交线所围成多边形的面积与三角形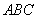 的面积之比。
的面积之比。

查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
如图,沿等腰直角三角形![]() 的中位线
的中位线![]() ,将平面
,将平面![]() 折起(转动一定角度),得到四棱锥
折起(转动一定角度),得到四棱锥![]() ,设
,设![]() 、
、![]() 、
、![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() 、
、![]() 、
、![]() ,平面
,平面![]() ⊥平面
⊥平面![]() 。
。
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)求证:![]() 、
、![]() 、
、![]() 、
、![]() 四点共面;
四点共面;


 (3)求异面直线
(3)求异面直线![]() 与
与![]() 所有的角。
所有的角。
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com