
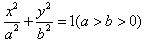 的两个焦点为F1、F2,点P在椭圆G上,且PF1⊥F1F2,且
的两个焦点为F1、F2,点P在椭圆G上,且PF1⊥F1F2,且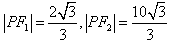 ,斜率为1的直线l与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(-3,2),
,斜率为1的直线l与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(-3,2), 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014届陕西省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
已知椭圆C: 的两个焦点为F1、F2,点P在椭圆C上,且|PF1|=
的两个焦点为F1、F2,点P在椭圆C上,且|PF1|= ,
,
|PF2|= , PF1⊥F1F2.
, PF1⊥F1F2.
(1)求椭圆C的方程;(6分)
(2)若直线L过圆x2+y2+4x-2y=0的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线L的方程.
查看答案和解析>>
科目:高中数学 来源:2013届广东省汕头市高二第一学期期末考试理科数学试卷 题型:解答题
已知椭圆C: 的两个焦点为
的两个焦点为 、
、
 ,且经过点
,且经过点 ,一组斜率为
,一组斜率为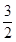 的直线与椭圆C都相交于不同两点
的直线与椭圆C都相交于不同两点 、
、 。
。
(1)求椭圆C的方程;
(2)证明:线段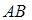 的中点都有在同一直线
的中点都有在同一直线 上;
上;
(3)对于(2)中的直线 ,设
,设 与椭圆C交于两点M、N,试探究椭圆上使
与椭圆C交于两点M、N,试探究椭圆上使 MNQ面积为
MNQ面积为 的点Q有几个?证明你的结论。(不必具体求出Q点的坐标)
的点Q有几个?证明你的结论。(不必具体求出Q点的坐标)
查看答案和解析>>
科目:高中数学 来源:2009-2010学年吉林省长春市东北师大附中高二(上)期末数学试卷(文科)(解析版) 题型:解答题
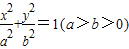 的两个焦点为F1(-1,0),F2(1,0),点
的两个焦点为F1(-1,0),F2(1,0),点 在椭圆C上.
在椭圆C上.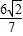 ,求直线l的方程.
,求直线l的方程.查看答案和解析>>
科目:高中数学 来源:2009-2010学年吉林省长春市东北师大附中高二(上)期末数学试卷(理科)(解析版) 题型:解答题
 的两个焦点为F1(-1,0),F2(1,0),点
的两个焦点为F1(-1,0),F2(1,0),点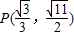 在椭圆C上.
在椭圆C上. ,求直线l的方程.
,求直线l的方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com