
|
解:(1)设M表示事件“恰有两个区域用红色鲜花”, |
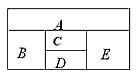 | ||||||||
| (2)随机变量ξ的取值分别为0,1,2, 则当ξ=0时,用黄、蓝、白、橙四种颜色来涂色, 若A、D为同色时,共有4×3×2×1×2=48种; 若A、D为不同色时,共有4×3×2×1×1=24种; 即ξ=0所包含的基本事件有48+24=72种, 所以, 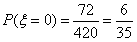 , ,由(1)知, 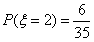 , ,所以 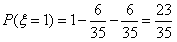 , ,从而随机变量ξ的分布列为:
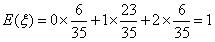 。 。 |


科目:高中数学 来源: 题型:
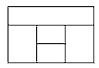
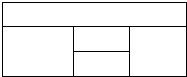 [理]用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图所示的花圃,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.
[理]用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图所示的花圃,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省南充市高三第二次诊断性考试理科数学卷 题型:解答题
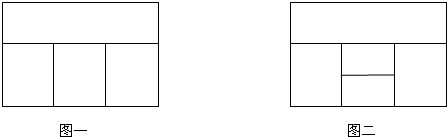
用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图所示的花圃(不一定用完每一种颜色的鲜花),要求同一区域上用同一种颜色的鲜花,相邻区域用不同颜色的鲜花.
①求恰有两个区域用红色鲜花的概率;
②记花圃中红色鲜花区域的块数为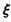 求
求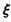 的分布列和数学期望E
的分布列和数学期望E
查看答案和解析>>
科目:高中数学 来源:2010-2011年江苏省如皋市五校高二下学期期中考试理科数学 题型:解答题
((本题16分)
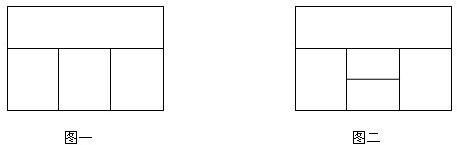
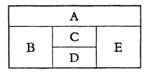
(1)用红、黄、蓝、白四种不同颜色的鲜花布置如图一所示的花圃,要求同一区域上用同一种颜色鲜花,相邻区域用不同颜色鲜花,问共有多少种不同的摆放方案?
(2)用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图二所示的花圃,要求同一区域上用同一种颜色鲜花,相邻区域使用不同颜色鲜花.

①求恰有两个区域用红色鲜花的概率;
②记花圃中红色鲜花区域的块数为S,求它的分布列及其数学期望E(S).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com