
((本题16分)
(1)用红、黄、蓝、白四种不同颜色的鲜花布置如图一所示的花圃,要求同一区域上用同一种颜色鲜花,相邻区域用不同颜色鲜花,问共有多少种不同的摆放方案?
(2)用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图二所示的花圃,要求同一区域上用同一种颜色鲜花,相邻区域使用不同颜色鲜花.

①求恰有两个区域用红色鲜花的概率;
②记花圃中红色鲜花区域的块数为S,求它的分布列及其数学期望E(S).
(1)根据分步计数原理,摆放鲜花的不同方案有: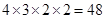 种.、、、、、、 6分
种.、、、、、、 6分
(2)① 设M表示事件“恰有两个区域用红色鲜花”,
如图二,当区域A、D同色时,共有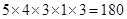 种;
种;
当区域A、D不同色时,共有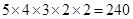 种;因此,所有基本事件总数为:180+240=420种.(由于只有A、D,B、E可能同色,故可按选用3色、4色、5色分类计算,求出基本事件总数为
种;因此,所有基本事件总数为:180+240=420种.(由于只有A、D,B、E可能同色,故可按选用3色、4色、5色分类计算,求出基本事件总数为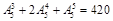 种)它们是等可能的。又因为A、D为红色时,共有
种)它们是等可能的。又因为A、D为红色时,共有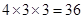 种;B、E为红色时,共有
种;B、E为红色时,共有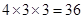 种;因此,事件M包含的基本事件有:36+36=72种.所以,
种;因此,事件M包含的基本事件有:36+36=72种.所以,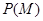 =
=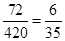 . 、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、12分
. 、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、12分
②随机变量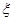 的分布列为:
的分布列为:
|
|
0 |
1 |
2 |
|
P |
|
|
|
所以,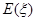 =
= .、、、、、、、、、、、、、、、、、、、、、、、、16分
.、、、、、、、、、、、、、、、、、、、、、、、、16分
【解析】略


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
(本题16分)已知椭圆C1:![]() 上的点满足到两焦点的距离之和为4,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点。
上的点满足到两焦点的距离之和为4,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点。
(1) 求双曲线C2的方程;
(2) 若以椭圆的右顶点为圆心,该椭圆的焦距为半径作一个圆,一条过点P(1,1)直线与该圆相交,交点为A、B,求弦AB最小时直线AB的方程,求求此时弦AB的长。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题16分)已知函数![]() 有如下性质:如果常数
有如下性质:如果常数![]() ,那么该函数在
,那么该函数在![]() 上是减函数,在
上是减函数,在![]() 上是增函数。
上是增函数。
(1)如果函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,求
上是增函数,求![]() 的值。
的值。
(2)设常数![]() ,求函数
,求函数![]() 的最大值和最小值;
的最大值和最小值;
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省宁波市金兰合作组织高三上学期期中联考文科数学试卷(解析版) 题型:解答题
(本题16分)已知函数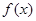 满足满足
满足满足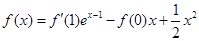 ;
;
(1)求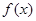 的解析式及单调区间;
的解析式及单调区间;
(2)若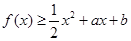 ,求
,求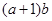 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:江苏省09-10学年度第一学期第三次月考高一数学 题型:解答题
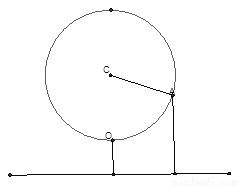
(本题16分)如图,某大风车的半径为2米,每12秒沿逆时针方向旋转一周,它的最底点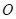 离地面1米,风车圆周上一点A从最底点
离地面1米,风车圆周上一点A从最底点 开始,运动t秒后与地面距离为h米,
开始,运动t秒后与地面距离为h米,
(1)求函数h=f(t)的关系式, 并在给出的方格纸上用五点作图法作出h=f(t)在一个周期内的图象(要列表,描点);
(2) A从最底点 开始, 沿逆时针方向旋转第一周内,有多长时间离地面的高度超过4米?
开始, 沿逆时针方向旋转第一周内,有多长时间离地面的高度超过4米?

查看答案和解析>>
科目:高中数学 来源:2010届上海市虹口区高三第二次模拟考试数学卷 题型:解答题
(本题16分)
如图所示,某人在斜坡P处仰视正对面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为 ,
,
(1)以射线OC为 轴的正向,OB为
轴的正向,OB为 轴正向,建立直角坐标系,求出斜坡CD所在直线方程;
轴正向,建立直角坐标系,求出斜坡CD所在直线方程;
(2)当观察者P视角∠APB最大时,求点P的坐标(人的身高忽略不计).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com