
(本题16分)已知函数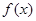 满足满足
满足满足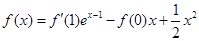 ;
;
(1)求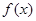 的解析式及单调区间;
的解析式及单调区间;
(2)若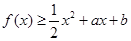 ,求
,求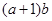 的最大值.
的最大值.
(1)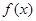 的解析式为
的解析式为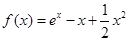 ,单调递增区间为
,单调递增区间为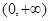 ,单调递减区间为
,单调递减区间为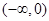 ;(2)
;(2)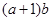 的最大值为
的最大值为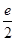
【解析】利用导数与函数单调性的关系求解单调区间以及利用导数求解函数的最值求解。
试题分析:
(1)
令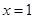 得:
得: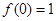
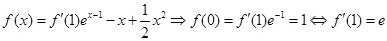
得: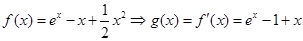
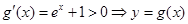 在
在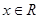 上单调递增
上单调递增
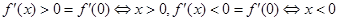
得: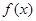 的解析式为
的解析式为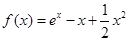
且单调递增区间为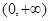 ,单调递减区间为
,单调递减区间为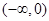 ……………8分
……………8分
(2)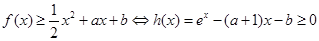 得
得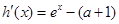
①当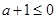 时,
时,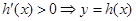 在
在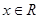 上单调递增
上单调递增
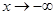 时,
时,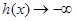 与
与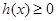 矛盾
矛盾
②当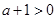 时,
时,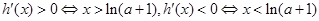
得:当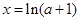 时,
时,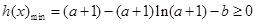
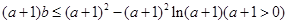
令 ;则
;则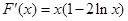
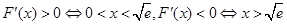
当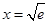 时,
时,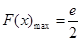
当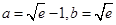 时,
时,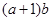 的最大值为
的最大值为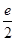 ………………………16分
………………………16分
考点:本题主要考查了利用导数与函数单调性的关系求解单调区间以及利用导数求解函数的最值等知识,综合考查了学生的运算求解能力和推理论证能力以及转化意识。
点评:解决此题的关键是熟练掌握利用导数与函数单调性的关系求解单调区间以及利用导数求解函数的最值的方法,以及较强的逻辑推理、运算求解及转化能力,难度很大。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2011-2012学年上海市高级中高三第二次月考试卷数学 题型:解答题
(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.
已知函数 是奇函数,定义域为区间D(使表达式有意义的实数x
的集合).
是奇函数,定义域为区间D(使表达式有意义的实数x
的集合).
(1)求实数m的值,并写出区间D;
(2)若底数 ,试判断函数
,试判断函数 在定义域D内的单调性,并证明;
在定义域D内的单调性,并证明;
(3)当 (
( ,a是底数)时,函数值组成的集合为
,a是底数)时,函数值组成的集合为 ,求实数
,求实数 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.
已知函数是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).
(1)求实数m的值,并写出区间D;
(2)若底数,试判断函数在定义域D内的单调性,并说明理由;
(3)当(,a是底数)时,函数值组成的集合为,求实数的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分)本题共有2个小题,第1小题满分7分,第2小题满分9分.
已知![]()
![]() 是偶函数.
是偶函数.
求b的值;
若在函数定义域内总存在区间![]() (m<n),使得
(m<n),使得![]() 在区间
在区间![]() 上的函数值组成的集合也是
上的函数值组成的集合也是![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.
已知函数是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).
(1)求实数m的值,并写出区间D;
(2)若底数,试判断函数在定义域D内的单调性,并说明理由;
(3)当(,a是底数)时,函数值组成的集合为,求实数的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分)本题共有2个小题,第1小题满分7分,第2小题满分9分.
已知![]()
![]() 是偶函数.
是偶函数.
求b的值;
若在函数定义域内总存在区间![]() (m<n),使得
(m<n),使得![]() 在区间
在区间![]() 上的函数值组成的集合也是
上的函数值组成的集合也是![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com