练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    简答题

    解不等式||＋|log3(3－x)|≥1．

    答案：
    解析：

    　　解：要使原不等式有意义，则即0＜x＜3．

    　　令＝0得x＝1，令log3(3－x)＝0，则x＝2．

    　　(1)当0＜x≤1时，原不等式可化为－log3x＋log3(3－x)≥1．

    　　∴log3(3－x)≥1＋log3x＝log3(3x)，

    　　∴3－x≥3x，∴x≤，故0＜x≤．

    　　(2)当1＜x＜2时，原不等式可化为log3x＋log3(3－x)≥1．

    　　即log3[x(3－x)]≥1，∴x(3－x)≥3．

    　　即x2－3x＋3≤0．此不等式无解．

    　　(3)当2≤x＜3时，原不等式可化为log3x－log3(3－x)≥1，即log3x≥1＋log3(3－x)

    　　∴log3x≥log3[3(3－x)]，∴x≥3(3－x)，∴x≥．

    　　故≤x＜3．

    　　综上可得，原不等式的解集为{x|0＜x≤或≤x＜3}．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：广东省高州一中2007届高三级数学(文科)(期中)考试题 题型：044

    简答题

    已知函数f(x)＝x2－4ax＋a2(a∈R)

    (1)

    若关于x的不等式f(x)≥x的解集为R，求实数a的取值范围；

    (2)

    若函数g(x)＝2x3＋3af(x)在内单调递增，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2015届浙江省高一上学期期末考试数学试卷（解析版） 题型：解答题

    已知定义在实数集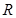上的奇函数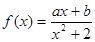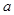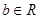（、）过已知点．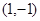

    （Ⅰ）求函数的解析式；

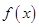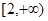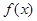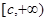    （Ⅱ）试证明函数在区间是增函数；若函数在区间（其中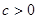）也是增函数，求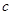的最小值；

    （Ⅲ）试讨论这个函数的单调性，并求它的最大值、最小值，在给出的坐标系（见答题卡）中画出能体现主要特征的图简；

    （Ⅳ）求不等式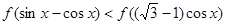的解集．

     

    查看答案和解析>>

    同步练习册答案