
【题目】为了了解高一学生的心理健康状况,某校心理健康咨询中心对该校高一学生的睡眠状况进行了抽样调查.该中心随机抽取了60名高一男生和40名高一女生,统计了他们入学第一个月的平均每天睡眠时间,得到如下频数分布表.规定:“平均每天睡眠时间大于等于8小时”为“睡眠充足”,“平均每天睡眠时间小于8小时”为“睡眠不足”.
高一男生平均每天睡眠时间频数分布表
睡眠时间(小时) |
|
|
|
|
|
频数 | 3 | 20 | 19 | 10 | 8 |
高一女生平均每天睡眠时间频数分布表
睡眠时间(小时) |
|
|
|
|
|
频数 | 20 | 11 | 5 | 2 |
(1)请将下面的列联表补充完整,并根据已完成的![]() 列联表,判断是否有
列联表,判断是否有![]() 的把握认为“睡眠是否充足与性别有关”?
的把握认为“睡眠是否充足与性别有关”?
睡眠充足 | 睡眠不足 | 合计 | |
男生 | 42 | ||
女生 | 7 | ||
合计 | 100 |
(2)由样本估计总体的思想,根据这两个频数分布表估计该校全体高一学生入学第一个月的平均每天睡眠时间(同一组中的数据以这组数据所在区间中点的值作代表);
(3)若再从这100人中平均每天睡眠时间不足6小时的同学里随机抽取两人进行心理健康干预,则抽取的两人中包含女生的概率是多少?
附:参考公式:![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【答案】(1)详见解析;(2)7.35小时;(3)![]() .
.
【解析】
(1)补全列联表,计算![]() ,然后与临界值表比较即可得到结论;(2)利用每个矩形的底边的中点横坐标与对应的小矩形的面积的乘积,然后作和,即可得到平均值;(3)利用古典概型的概率公式计算即可.
,然后与临界值表比较即可得到结论;(2)利用每个矩形的底边的中点横坐标与对应的小矩形的面积的乘积,然后作和,即可得到平均值;(3)利用古典概型的概率公式计算即可.
解:(1)![]() 列联表如下:
列联表如下:
睡眠充足 | 睡眠不足 | 合计 | |
男生 | 18 | 42 | 60 |
女生 | 7 | 33 | 40 |
合计 | 25 | 75 | 100 |
由表中数据计算得:![]() ,
,
所以没有![]() 的把握认为“睡眠是否充足与性别有关”.
的把握认为“睡眠是否充足与性别有关”.
(2)由两个表格可知,在所抽取的100名高一学生中,平均每天睡眠时间在![]() 内的有5人,在
内的有5人,在![]() 内的有40人,在
内的有40人,在![]() 内的有30人,在
内的有30人,在![]() 内的有15人,在
内的有15人,在![]() 内的有10人,同一组中的数据以这组数据所在区间中点的值作代表,估计该校全体高一学生入学第一个月的平均每天睡眠时间为
内的有10人,同一组中的数据以这组数据所在区间中点的值作代表,估计该校全体高一学生入学第一个月的平均每天睡眠时间为
![]()
![]() (小时).
(小时).
(3)这100人中平均每天睡眠时间不足6小时的同学里有3名男生和2名女生.
记三名男生为“![]() ”,两名女生为“
”,两名女生为“![]() ”,
”,
从中选取两名同学可能情形为:![]() .
.
记事件“抽取的两人中包含女生”为事件![]() ,则
,则![]() .
.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1+a2+a3+…+an=n-an,(n=1,2,3,…)
(Ⅰ)求证:数列{an-1}是等比数列;
(Ⅱ)令bn=(2-n)(an-1)(n=1,2,3,…),如果对任意n∈N*,都有bn+![]() t≤t2,求实数t的取值范围.
t≤t2,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线;
处的切线;
(2)若函数![]() 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,若在
,若在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人们经济收入的不断增加,个人购买家庭轿车已不再是一种时尚,车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题,某汽车销售公司做了一次抽样调查,并统计得出2009年出售的某款车的使用年限![]() (2009年记
(2009年记![]() )与所支出的总费用
)与所支出的总费用![]() (万元)有如表的数据资料:
(万元)有如表的数据资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
总费用 | 2.5 | 3.5 | 5.5 | 6.5 | 7.0 |
(1)求线性回归方程![]() ;
;
(2)若这款车一直使用到2020年,估计使用该款车的总费用是多少元?
线性回归方程![]() 中斜率和截距用最小二乘法估计计算公式如下:
中斜率和截距用最小二乘法估计计算公式如下:
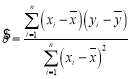
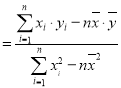 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() .
.
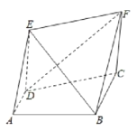
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两定点![]() ,
,![]() ,点P是平面内的动点,且
,点P是平面内的动点,且![]() ,记动点P的轨迹W.
,记动点P的轨迹W.
(1)求动点P的轨迹W的方程;
(2)过点![]() 作两条相垂直的直线分别交轨迹于G,H,M,N四点.设四边形GMHN面积为S,求
作两条相垂直的直线分别交轨迹于G,H,M,N四点.设四边形GMHN面积为S,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地种植常规稻![]() 和杂交稻
和杂交稻![]() ,常规稻
,常规稻![]() 的亩产稳定为485公斤,今年单价为3.70元/公斤,估计明年单价不变的可能性为
的亩产稳定为485公斤,今年单价为3.70元/公斤,估计明年单价不变的可能性为![]() ,变为3.90元/公斤的可能性为
,变为3.90元/公斤的可能性为![]() ,变为4.00的可能性为
,变为4.00的可能性为![]() .统计杂交稻
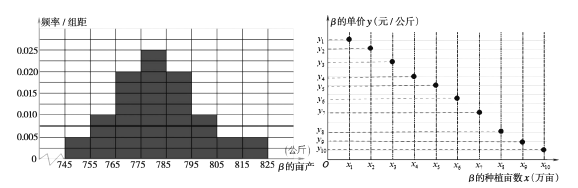
.统计杂交稻![]() 的亩产数据,得到亩产的频率分布直方图如图①.统计近10年杂交稻
的亩产数据,得到亩产的频率分布直方图如图①.统计近10年杂交稻![]() 的单价(单位:元/公斤)与种植亩数(单位:万亩)的关系,得到的10组数据记为
的单价(单位:元/公斤)与种植亩数(单位:万亩)的关系,得到的10组数据记为![]() ,并得到散点图如图②.
,并得到散点图如图②.
(1)根据以上数据估计明年常规稻![]() 的单价平均值;
的单价平均值;
(2)在频率分布直方图中,各组的取值按中间值来计算,求杂交稻![]() 的亩产平均值;以频率作为概率,预计将来三年中至少有二年,杂交稻
的亩产平均值;以频率作为概率,预计将来三年中至少有二年,杂交稻![]() 的亩产超过795公斤的概率;
的亩产超过795公斤的概率;
(3)①判断杂交稻![]() 的单价
的单价![]() (单位:元/公斤)与种植亩数
(单位:元/公斤)与种植亩数![]() (单位:万亩)是否线性相关?若相关,试根据以下的参考数据求出
(单位:万亩)是否线性相关?若相关,试根据以下的参考数据求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
②调查得知明年此地杂交稻![]() 的种植亩数预计为2万亩.若在常规稻
的种植亩数预计为2万亩.若在常规稻![]() 和杂交稻
和杂交稻![]() 中选择,明年种植哪种水稻收入更高?
中选择,明年种植哪种水稻收入更高?
统计参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
附:线性回归方程![]() ,
,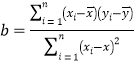 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,
,![]() 是椭圆上关于原点
是椭圆上关于原点![]() 对称的两个动点,当点
对称的两个动点,当点![]() 的坐标为
的坐标为![]() 时,
时,![]() 的周长恰为
的周长恰为![]() .
.
(1)求椭圆的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,且
两点,且![]()
![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com