
(本题满分14分)
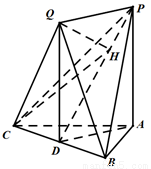
如图,已知平面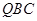 与直线
与直线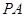 均垂直于
均垂直于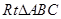 所在平面,且
所在平面,且 ,
,

(Ⅰ)求证: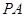
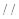 平面
平面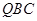 ;
;
(Ⅱ)若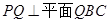 ,求
,求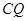 与平面
与平面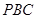 所成角的正弦值.
所成角的正弦值.
(Ⅰ)只需证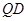 ∥
∥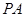 ;(Ⅱ)
;(Ⅱ)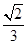 。
。
【解析】
试题分析:(Ⅰ)证明:过点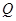 作
作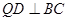 于点
于点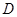 ,
,
∵平面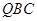 ⊥平面
⊥平面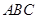 ,∴
,∴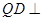 平面
平面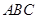 ……2分
……2分
又∵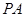 ⊥平面
⊥平面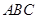
∴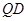 ∥
∥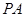 ,
………………2分
,
………………2分
又∵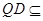 平面
平面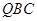
∴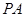 ∥平面
∥平面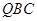 ………………6分
………………6分
(Ⅱ)∵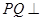 平面
平面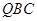 ∴
∴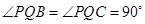 ,又∵
,又∵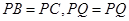 ∴
∴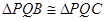 ∴
∴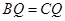 ………………8分
………………8分
∴点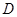 是
是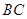 的中点,连结
的中点,连结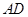 ,则
,则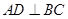
∴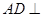 平面
平面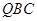 ∴
∴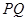 ∥
∥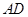 ,
,
∴四边形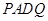 是矩形
………………10分
是矩形
………………10分
设 ,得:
,得: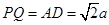 ,
,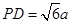
又∵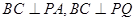 ,∴
,∴ ,
,
从而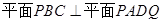 ,过
,过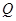 作
作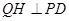 于点
于点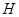 ,则:
,则: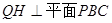
∴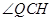 是
是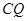 与平面
与平面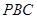 所成角
………………………………………………12分
所成角
………………………………………………12分
∴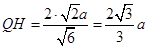 ,
,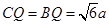
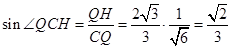
∴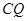 与平面
与平面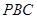 所成角的正弦值为
所成角的正弦值为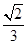 …………………………14分
…………………………14分
考点:面面垂直的性质定理;线面平行的判定定理;线面垂直的性质定理;直线与平面所成的角。
点评:本题主要考查了线面平行的证明和直线与平面所成的角,属立体几何中的常考题型,较难.本题也可以用向量法来做:用向量法解题的关键是;首先正确的建立空间直角坐标系,正确求解平面的一个法向量。注意计算要仔细、认真。


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:
| π |
| 3 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,![]() 为
为![]() 上的点,且BF⊥平面ACE.
上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE;(2)求三棱锥D-AEC的体积;(3)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三上学期期中考试数学 题型:解答题
(本题满分14分)已知集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}
(Ⅰ)若A B=[0,3],求实数m的值
B=[0,3],求实数m的值
(Ⅱ)若A CRB,求实数m的取值范围
CRB,求实数m的取值范围
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三上学期第三次月考理科数学卷 题型:解答题
(本题满分14分)
已知点 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 作
作 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。
(1)求动点 的轨迹方程;
的轨迹方程;
(2)已知点 ,在动点
,在动点 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2014届江西省高一第二学期入学考试数学 题型:解答题
(本题满分14分)已知函数 .
.
(1)求函数 的定义域;
的定义域;
(2)判断 的奇偶性;
的奇偶性;
(3)方程 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使

 ;如果没有,请说明理由?(注:区间的长度为
;如果没有,请说明理由?(注:区间的长度为 ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com