
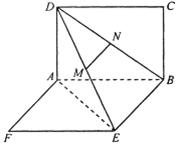
如图,两矩形ABCD,ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为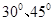 ,M、N分别为DE与DB的中点,且MN=1.
,M、N分别为DE与DB的中点,且MN=1.
(1) 求证:MN丄平面ABCD
(2) 求线段AB的长;
(3) 求二面角A—DE—B的平面角的正弦值.
(Ⅰ)证明:∵平面ABCD⊥平面ABEF,且平面ABCD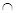 平面ABEF=AB
平面ABEF=AB
EB⊥AB ∴EB⊥平面ABCD 又MN∥EB
∴MN⊥面ABCD. (3分)
(Ⅱ)由(Ⅰ)可知∠EDB为DE与平面ABCD所成的角 ∴∠EDB=30o
又在Rt△EBD中,EB=2MN=2,∠EBD=90o
∴DE=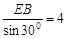
连结AE,可知∠DEA为DE与平面ABEF所成的角 ∴∠DEA=45o (5分)
在Rt△DAE中,∠DAE=90o
∴AE=DE cos∠DEA=2
在Rt△ABE中,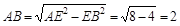 . (7分)
. (7分)

(Ⅲ)方法一:过B作BO⊥AE于O点,过O作OH⊥DE于H,连BH
∵AD⊥平面ABEF BO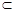 面ABEF
面ABEF
∴BO⊥平面ADE ∴OH为BH在平面ADE内的射影
∴BH⊥DE 即∠BHO为所求二面角的平面角 (9分)
在Rt△ABE中,BO=
在Rt△DBE中,由BH·DE=DB·OE得BH=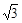
∴sin∠BHO=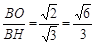
【解析】略


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
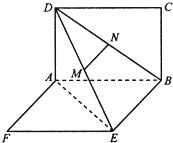 如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面所成角分别为300、450,M、N分别为DE与DB的中点,且MN=1.
如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面所成角分别为300、450,M、N分别为DE与DB的中点,且MN=1.查看答案和解析>>
科目:高中数学 来源: 题型:
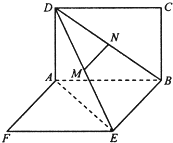 (2012•焦作模拟)如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1.
(2012•焦作模拟)如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1.查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川宜宾市高三第一次诊断性考试文科数学试卷(解析版) 题型:解答题
如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1.
(I) 求证:MN⊥平面ABCD

(II) 求线段AB的长;
(III)求二面角A-DE-B的平面角的正弦值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省焦作市高三第一次质量检测文科数学试卷(解析版) 题型:解答题
如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面所成角分别为300、450, M、N分别为DE与DB的中点,且MN=1.
(Ⅰ)求证:MN⊥平面ABCD;
(Ⅱ)求线段AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com