
| A. | f(sinα)>f(cosβ) | B. | f(cosα)>f(sinβ) | C. | f(sinα)<f(sinβ) | D. | f(cosα)<f(cosβ) |
分析 由题意可得锐角α,β满足$α+β<\frac{π}{2}$,由此求得sinα<cosβ,再由复合函数的单调性得答案.
解答 解:∵锐角α,β满足α+β$>\frac{π}{2}$,则$α>\frac{π}{2}-β$,sinα>sin($\frac{π}{2}-β$)=cosβ,∴$\frac{sinα}{cosβ}>1$,
同理$\frac{sinβ}{cosα}$>1,则$\frac{sinα}{cosβ}$+$\frac{sinβ}{cosα}$>2,与已知矛盾;
∴$α+β<\frac{π}{2}$.
即$α<\frac{π}{2}-β$,∴$sinα<sin(\frac{π}{2}-β)=cosβ$,
∵f(x)=logax(0<a<1)为减函数,
∴f(sinα)>f(cosβ).
故选:A.
点评 本题考查三角函数的单调性,考查三角函数值的大小比较,训练了复合函数单调性的判定方法,是中档题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:选择题
| A. | (3,-4) | B. | (3,-4),(-3,4) | C. | ($\frac{3}{5}$,一$\frac{4}{5}$) | D. | ($\frac{3}{5}$,一$\frac{4}{5}$),(一$\frac{3}{5}$,$\frac{4}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
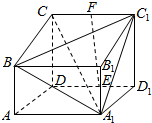 如图,四棱柱ABCD-A1B1C1D1中,侧面AA1D1D为矩形,AB⊥平面AA1D1D,CD⊥平面AA1D1D,E、F分别为A1B1、CC1的中点,且AA1=CD=2,AB=AD=1.
如图,四棱柱ABCD-A1B1C1D1中,侧面AA1D1D为矩形,AB⊥平面AA1D1D,CD⊥平面AA1D1D,E、F分别为A1B1、CC1的中点,且AA1=CD=2,AB=AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com